| << Chapter < Page | Chapter >> Page > |
Many real-world scenarios represent periodic functions and may be modeled by trigonometric functions. As an example, let’s return to the scenario from the section opener. Have you ever observed the beam formed by the rotating light on a police car and wondered about the movement of the light beam itself across the wall? The periodic behavior of the distance the light shines as a function of time is obvious, but how do we determine the distance? We can use the tangent function .
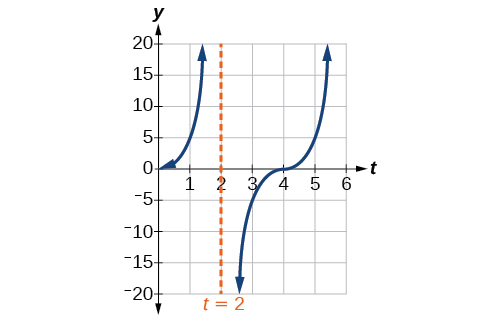
Suppose the function marks the distance in the movement of a light beam from the top of a police car across a wall where is the time in seconds and is the distance in feet from a point on the wall directly across from the police car.
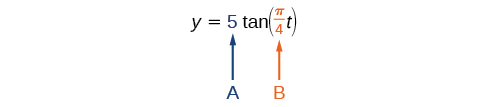
We see that the stretching factor is 5. This means that the beam of light will have moved 5 ft after half the period.
The period is This means that every 4 seconds, the beam of light sweeps the wall. The distance from the spot across from the police car grows larger as the police car approaches.
Access these online resources for additional instruction and practice with graphs of other trigonometric functions.
| Shifted, compressed, and/or stretched tangent function | |
| Shifted, compressed, and/or stretched secant function | |
| Shifted, compressed, and/or stretched cosecant function | |
| Shifted, compressed, and/or stretched cotangent function |
Explain how the graph of the sine function can be used to graph
Since is the reciprocal function of you can plot the reciprocal of the coordinates on the graph of to obtain the y -coordinates of The x -intercepts of the graph are the vertical asymptotes for the graph of

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?