| << Chapter < Page | Chapter >> Page > |
On many cell phones with GPS, an approximate location can be given before the GPS signal is received. This is accomplished through a process called triangulation, which works by using the distances from two known points. Suppose there are two cell phone towers within range of a cell phone. The two towers are located 6000 feet apart along a straight highway, running east to west, and the cell phone is north of the highway. Based on the signal delay, it can be determined that the signal is 5050 feet from the first tower and 2420 feet from the second tower. Determine the position of the cell phone north and east of the first tower, and determine how far it is from the highway.
For simplicity, we start by drawing a diagram similar to [link] and labeling our given information.
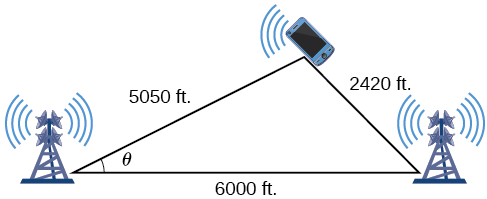
Using the Law of Cosines, we can solve for the angle Remember that the Law of Cosines uses the square of one side to find the cosine of the opposite angle. For this example, let and Thus, corresponds to the opposite side
To answer the questions about the phone’s position north and east of the tower, and the distance to the highway, drop a perpendicular from the position of the cell phone, as in [link] . This forms two right triangles, although we only need the right triangle that includes the first tower for this problem.
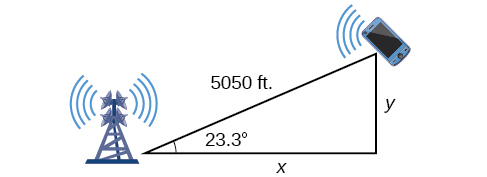
Using the angle and the basic trigonometric identities, we can find the solutions. Thus
The cell phone is approximately 4638 feet east and 1998 feet north of the first tower, and 1998 feet from the highway.
Returning to our problem at the beginning of this section, suppose a boat leaves port, travels 10 miles, turns 20 degrees, and travels another 8 miles. How far from port is the boat? The diagram is repeated here in [link] .
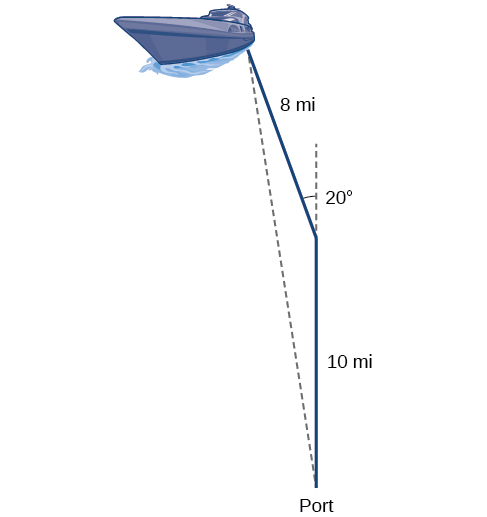
The boat turned 20 degrees, so the obtuse angle of the non-right triangle is the supplemental angle, With this, we can utilize the Law of Cosines to find the missing side of the obtuse triangle—the distance of the boat to the port.
The boat is about 17.7 miles from port.
We already learned how to find the area of an oblique triangle when we know two sides and an angle. We also know the formula to find the area of a triangle using the base and the height. When we know the three sides, however, we can use Heron’s formula instead of finding the height. Heron of Alexandria was a geometer who lived during the first century A.D. He discovered a formula for finding the area of oblique triangles when three sides are known.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?