| << Chapter < Page | Chapter >> Page > |
Given two sides and the angle between them (SAS), find the measures of the remaining side and angles of a triangle.
Find the unknown side and angles of the triangle in [link] .
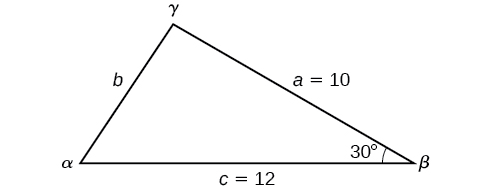
First, make note of what is given: two sides and the angle between them. This arrangement is classified as SAS and supplies the data needed to apply the Law of Cosines.
Each one of the three laws of cosines begins with the square of an unknown side opposite a known angle. For this example, the first side to solve for is side as we know the measurement of the opposite angle
Because we are solving for a length, we use only the positive square root. Now that we know the length we can use the Law of Sines to fill in the remaining angles of the triangle. Solving for angle we have
The other possibility for would be In the original diagram, is adjacent to the longest side, so is an acute angle and, therefore, does not make sense. Notice that if we choose to apply the Law of Cosines , we arrive at a unique answer. We do not have to consider the other possibilities, as cosine is unique for angles between and Proceeding with we can then find the third angle of the triangle.
The complete set of angles and sides is
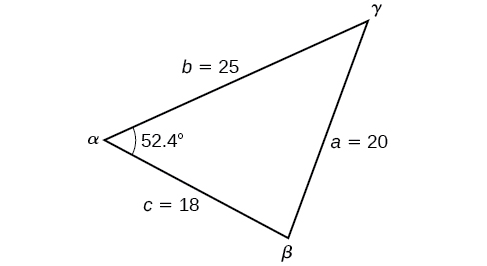
Find the angle for the given triangle if side side and side
For this example, we have no angles. We can solve for any angle using the Law of Cosines. To solve for angle we have
See [link] .
Just as the Law of Sines provided the appropriate equations to solve a number of applications, the Law of Cosines is applicable to situations in which the given data fits the cosine models. We may see these in the fields of navigation, surveying, astronomy, and geometry, just to name a few.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?