| << Chapter < Page | Chapter >> Page > |
Given a logarithmic function with the parent function graph a translation.
|
|
|
|
|
|
|
|
|
|
Sketch a graph of alongside its parent function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.
Before graphing identify the behavior and key points for the graph.
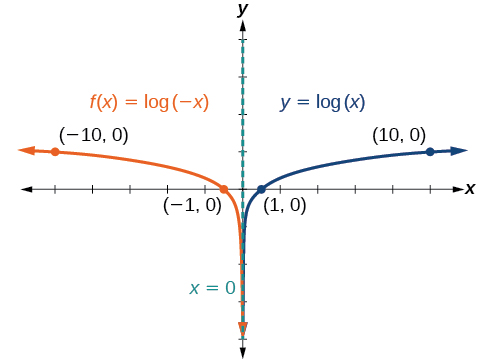
The domain is the range is and the vertical asymptote is
Graph State the domain, range, and asymptote.
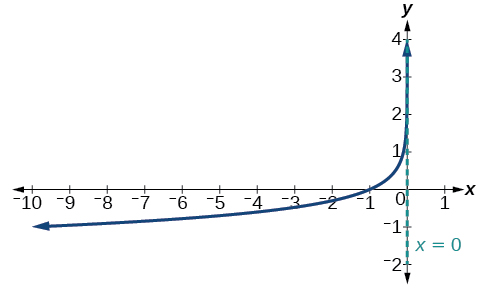
The domain is the range is and the vertical asymptote is
Given a logarithmic equation, use a graphing calculator to approximate solutions.
Solve graphically. Round to the nearest thousandth.
Press [Y=] and enter next to Y 1 =. Then enter next to Y 2 = . For a window, use the values 0 to 5 for and –10 to 10 for Press [GRAPH] . The graphs should intersect somewhere a little to right of
For a better approximation, press [2ND] then [CALC] . Select [5: intersect] and press [ENTER] three times. The x -coordinate of the point of intersection is displayed as 1.3385297. (Your answer may be different if you use a different window or use a different value for Guess? ) So, to the nearest thousandth,
Now that we have worked with each type of translation for the logarithmic function, we can summarize each in [link] to arrive at the general equation for translating exponential functions.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?