| << Chapter < Page | Chapter >> Page > |
The inverse of every logarithmic function is an exponential function and vice-versa. What does this tell us about the relationship between the coordinates of the points on the graphs of each?
Since the functions are inverses, their graphs are mirror images about the line So for every point on the graph of a logarithmic function, there is a corresponding point on the graph of its inverse exponential function.
What type(s) of translation(s), if any, affect the range of a logarithmic function?
What type(s) of translation(s), if any, affect the domain of a logarithmic function?
Shifting the function right or left and reflecting the function about the y-axis will affect its domain.
Consider the general logarithmic function Why can’t be zero?
Does the graph of a general logarithmic function have a horizontal asymptote? Explain.
No. A horizontal asymptote would suggest a limit on the range, and the range of any logarithmic function in general form is all real numbers.
For the following exercises, state the domain and range of the function.
For the following exercises, state the domain and the vertical asymptote of the function.
For the following exercises, state the domain, vertical asymptote, and end behavior of the function.
For the following exercises, state the domain, range, and x - and y -intercepts, if they exist. If they do not exist, write DNE.
Domain: Range: Vertical asymptote: x -intercept: y -intercept: DNE
Domain: Range: Vertical asymptote: x -intercept: y -intercept: DNE
Domain: Range: Vertical asymptote: x -intercept: y -intercept: DNE
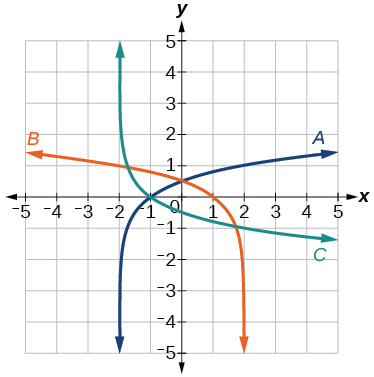
For the following exercises, match each function in [link] with the letter corresponding to its graph.
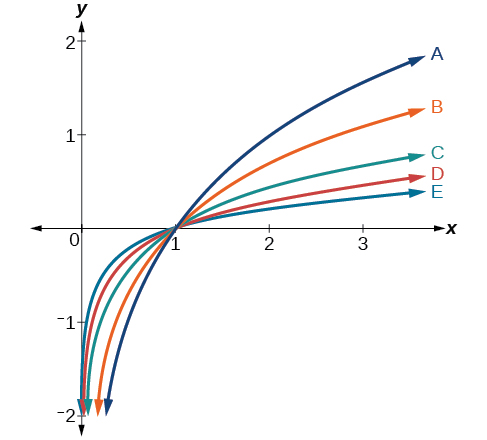
For the following exercises, match each function in [link] with the letter corresponding to its graph.
For the following exercises, sketch the graphs of each pair of functions on the same axis.
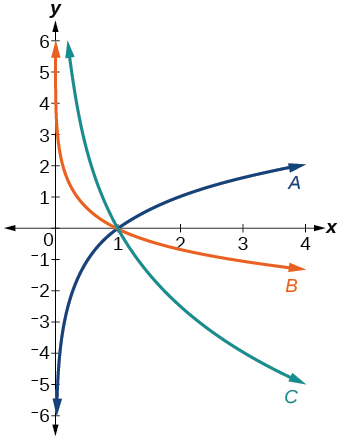
For the following exercises, match each function in [link] with the letter corresponding to its graph.
For the following exercises, sketch the graph of the indicated function.
For the following exercises, write a logarithmic equation corresponding to the graph shown.
Use as the parent function.
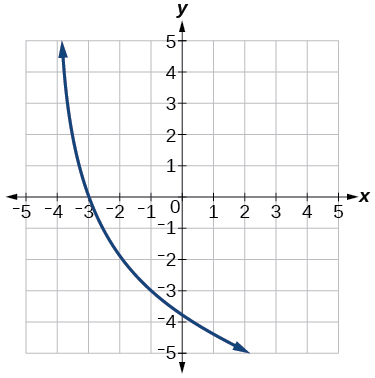
Use as the parent function.
For the following exercises, use a graphing calculator to find approximate solutions to each equation.
Let be any positive real number such that What must be equal to? Verify the result.
Explore and discuss the graphs of and Make a conjecture based on the result.
The graphs of and appear to be the same; Conjecture: for any positive base
Prove the conjecture made in the previous exercise.
What is the domain of the function Discuss the result.
Recall that the argument of a logarithmic function must be positive, so we determine where . From the graph of the function note that the graph lies above the x -axis on the interval and again to the right of the vertical asymptote, that is Therefore, the domain is

Use properties of exponents to find the x -intercepts of the function algebraically. Show the steps for solving, and then verify the result by graphing the function.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?