7.5 Solving trigonometric equations  (Page 5/7)

If we rewrite the right side, we can write the equation in terms of cosine:

Our solutions are $\frac{2\pi }{3},\frac{4\pi }{3},\pi .$

We can see that this equation is the standard equation with a multiple of an angle. If $\cos \left(\alpha \right)=\frac{1}{2},$ we know $\alpha$ is in quadrants I and IV. While $\theta ={\cos }^{-1}\frac{1}{2}$ will only yield solutions in quadrants I and II, we recognize that the solutions to the equation $\cos \theta =\frac{1}{2}$ will be in quadrants I and IV.

Therefore, the possible angles are $\theta =\frac{\pi }{3}$ and $\theta =\frac{5\pi }{3}.$ So, $2x=\frac{\pi }{3}$ or $2x=\frac{5\pi }{3},$ which means that $x=\frac{\pi }{6}$ or $x=\frac{5\pi }{6}.$ Does this make sense? Yes, because $\cos \left(2\left(\frac{\pi }{6}\right)\right)=\cos \left(\frac{\pi }{3}\right)=\frac{1}{2}.$

Are there any other possible answers? Let us return to our first step.

In quadrant I, $2x=\frac{\pi }{3},$ so $x=\frac{\pi }{6}$ as noted. Let us revolve around the circle again:

so $x=\frac{7\pi }{6}.$

One more rotation yields

$x=\frac{13\pi }{6}>2\pi ,$ so this value for $x$ is larger than $2\pi ,$ so it is not a solution on $\left[0,2\pi \right).$

In quadrant IV, $2x=\frac{5\pi }{3},$ so $x=\frac{5\pi }{6}$ as noted. Let us revolve around the circle again:

so $x=\frac{11\pi }{6}.$

One more rotation yields

$x=\frac{17\pi }{6}>2\pi ,$ so this value for $x$ is larger than $2\pi ,$ so it is not a solution on $\left[0,2\pi \right).$

Our solutions are $\frac{\pi }{6},\frac{5\pi }{6},\frac{7\pi }{6},\text{and }\frac{11\pi }{6}.$ Note that whenever we solve a problem in the form of $\sin \left(nx\right)=c,$ we must go around the unit circle $n$ times.

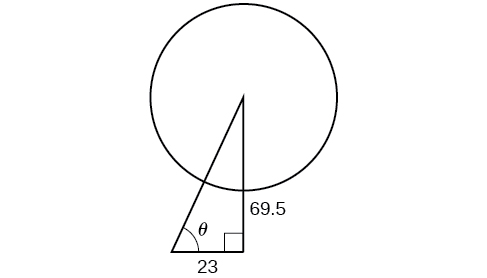
Using the information given, we can draw a right triangle. We can find the length of the cable with the Pythagorean Theorem.

The angle of elevation is $\theta ,$ formed by the second anchor on the ground and the cable reaching to the center of the wheel. We can use the tangent function to find its measure. Round to two decimal places.

The angle of elevation is approximately ${71.7}^{\circ },$ and the length of the cable is 73.2 meters.