| << Chapter < Page | Chapter >> Page > |
Identify all exact solutions to the equation
We can solve this equation using only algebra. Isolate the expression on the left side of the equals sign.
There are two angles on the unit circle that have a tangent value of and
Not all functions can be solved exactly using only the unit circle. When we must solve an equation involving an angle other than one of the special angles, we will need to use a calculator. Make sure it is set to the proper mode, either degrees or radians, depending on the criteria of the given problem.
Use a calculator to solve the equation where is in radians.
Make sure mode is set to radians. To find use the inverse sine function. On most calculators, you will need to push the 2 ND button and then the SIN button to bring up the function. What is shown on the screen is The calculator is ready for the input within the parentheses. For this problem, we enter and press ENTER. Thus, to four decimals places,
The solution is
The angle measurement in degrees is
Use a calculator to solve the equation giving your answer in radians.
We can begin with some algebra.
Check that the MODE is in radians. Now use the inverse cosine function.
Since and 1.8235 is between these two numbers, thus is in quadrant II. Cosine is also negative in quadrant III. Note that a calculator will only return an angle in quadrants I or II for the cosine function, since that is the range of the inverse cosine. See [link] .
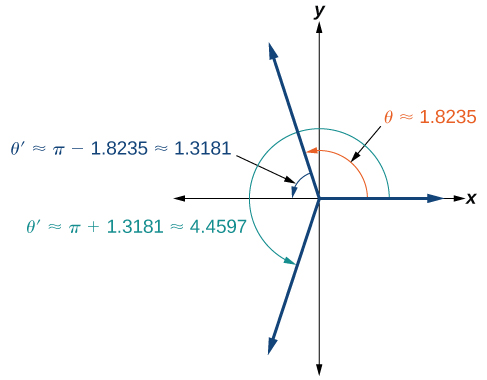
So, we also need to find the measure of the angle in quadrant III. In quadrant III, the reference angle is The other solution in quadrant III is
The solutions are and
Solving a quadratic equation may be more complicated, but once again, we can use algebra as we would for any quadratic equation. Look at the pattern of the equation. Is there more than one trigonometric function in the equation, or is there only one? Which trigonometric function is squared? If there is only one function represented and one of the terms is squared, think about the standard form of a quadratic. Replace the trigonometric function with a variable such as or If substitution makes the equation look like a quadratic equation, then we can use the same methods for solving quadratics to solve the trigonometric equations.
Solve the equation exactly:
We begin by using substitution and replacing cos with It is not necessary to use substitution, but it may make the problem easier to solve visually. Let We have
The equation cannot be factored, so we will use the quadratic formula
Replace with and solve. Thus,
Note that only the + sign is used. This is because we get an error when we solve on a calculator, since the domain of the inverse cosine function is However, there is a second solution:
This terminal side of the angle lies in quadrant I. Since cosine is also positive in quadrant IV, the second solution is

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?