7.6 Modeling with trigonometric equations (Page 6/14)

Precalculus

Page 6 / 14

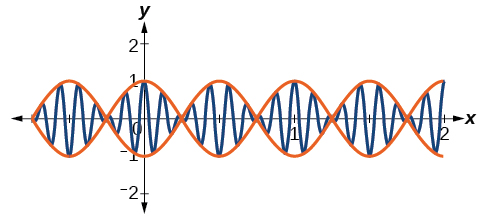
Bounding curves in harmonic motion

Harmonic motion graphs may be enclosed by bounding curves. When a function has a varying amplitude , such that the amplitude rises and falls multiple times within a period, we can determine the bounding curves from part of the function.

Graphing an oscillating cosine curve

Graph the function $f (x) = \cos (2 π x) \cos (16 π x) .$

The graph produced by this function will be shown in two parts. The first graph will be the exact function $f (x)$ (see [link] ), and the second graph is the exact function $f (x)$ plus a bounding function (see [link] . The graphs look quite different.

Graph of f(x) = cos(2pi*x)cos(16pi*x), a sinusoidal function that increases and decreases its amplitude periodically.

Graph of f(x) = cos(2pi*x)cos(16pi*x), a sinusoidal function that increases and decreases its amplitude periodically. There is also a bonding function drawn over it in red, which makes the whole image look like a DNA (double helix) piece stretched along the x-axis.

Got questions? Get instant answers now!

Media

Access these online resources for additional instruction and practice with trigonometric applications.

Visit this website for additional practice questions from Learningpod.

Key equations


Standard form of sinusoidal equation	$y = A \sin (B t - C) + D or y = A \cos (B t - C) + D$
Simple harmonic motion	$d = a \cos (ω t) or d = a \sin (ω t)$
Damped harmonic motion	$f (t) = a e^{- c}^{t} \sin (ω t) or f (t) = a e^{- c t} \cos (ω t)$

Key concepts

Sinusoidal functions are represented by the sine and cosine graphs. In standard form, we can find the amplitude, period, and horizontal and vertical shifts. See [link] and [link] .
Use key points to graph a sinusoidal function. The five key points include the minimum and maximum values and the midline values. See [link] .
Periodic functions can model events that reoccur in set cycles, like the phases of the moon, the hands on a clock, and the seasons in a year. See [link] , [link] , [link] and [link] .
Harmonic motion functions are modeled from given data. Similar to periodic motion applications, harmonic motion requires a restoring force. Examples include gravitational force and spring motion activated by weight. See [link] .
Damped harmonic motion is a form of periodic behavior affected by a damping factor. Energy dissipating factors, like friction, cause the displacement of the object to shrink. See [link] , [link] , [link] , [link] , and [link] .
Bounding curves delineate the graph of harmonic motion with variable maximum and minimum values. See [link] .

Section exercises

Verbal

Explain what types of physical phenomena are best modeled by sinusoidal functions. What are the characteristics necessary?

Physical behavior should be periodic, or cyclical.

Got questions? Get instant answers now!

What information is necessary to construct a trigonometric model of daily temperature? Give examples of two different sets of information that would enable modeling with an equation.

Got questions? Get instant answers now!

If we want to model cumulative rainfall over the course of a year, would a sinusoidal function be a good model? Why or why not?

Since cumulative rainfall is always increasing, a sinusoidal function would not be ideal here.

Got questions? Get instant answers now!

Explain the effect of a damping factor on the graphs of harmonic motion functions.

Got questions? Get instant answers now!

Algebraic

For the following exercises, find a possible formula for the trigonometric function represented by the given table of values.


$x$	$y$
$0$	$- 4$
$3$	$- 1$
$6$	$2$
$9$	$- 1$
$12$	$- 4$
$15$	$- 1$
$18$	$2$

$y = - 3 \cos (\frac{π}{6} x) - 1$

Got questions? Get instant answers now!


$x$	$y$
$0$	$5$
$2$	$1$
$4$	$- 3$
$6$	$1$
$8$	$5$
$10$	$1$
$12$	$- 3$

Got questions? Get instant answers now!


$x$	$y$
$0$	$2$
$\frac{π}{4}$	$7$
$\frac{π}{2}$	$2$
$\frac{3 π}{4}$	$- 3$
$π$	$2$
$\frac{5 π}{4}$	$7$
$\frac{3 π}{2}$	$2$

$5 \sin (2 x) + 2$

Got questions? Get instant answers now!


$x$	$y$
$0$	$2$
$\frac{π}{4}$	$7$
$\frac{π}{2}$	$2$
$\frac{3 π}{4}$	$- 3$
$π$	$2$
$\frac{5 π}{4}$	$7$
$\frac{3 π}{2}$	$2$

Got questions? Get instant answers now!


$x$	$y$
$0$	$1$
$1$	$- 3$
$2$	$- 7$
$3$	$- 3$
$4$	$1$
$5$	$- 3$
$6$	$- 7$

$4 \cos (\frac{x π}{2}) - 3$

Got questions? Get instant answers now!


$x$	$y$
$0$	$- 2$
$1$	$4$
$2$	$10$
$3$	$4$
$4$	$- 2$
$5$	$4$
$6$	$10$

Got questions? Get instant answers now!

Questions & Answers

why we learn economics ? Explain briefly

ayalew Reply

why we learn economics ?

ayalew

why we learn economics

ayalew

profit maximize for monopolistically?

Usman Reply

what kind of demand curve under monopoly?

Mik Reply

what is the difference between inflation and scarcity ?

Abdu Reply

What stops oligopolists from acting together as a monopolist and earning the highest possible level of profits?

Mik

why economics is difficult for 2nd school students.

Siraj Reply

what does mean opportunity cost?

Aster Reply

what is poetive effect of population growth

Solomon Reply

what is inflation

Nasir Reply

what is demand

Eleni

what is economics

IMLAN Reply

economics theory describes individual behavior as the result of a process of optimization under constraints the objective to be reached being determined by

Kalkidan

Economics is a branch of social science that deal with How to wise use of resource ,s

Kassie

need

WARKISA

Economic Needs: In economics, needs are goods or services that are necessary for maintaining a certain standard of living. This includes things like healthcare, education, and transportation.

Kalkidan

What is demand and supply

EMPEROR Reply

deman means?

Alex

what is supply?

Alex

ex play supply?

Alex

Money market is a branch or segment of financial market where short-term debt instruments are traded upon. The instruments in this market includes Treasury bills, Bonds, Commercial Papers, Call money among other.

murana Reply

good

Kayode

what is money market

umar Reply

Examine the distinction between theory of comparative cost Advantage and theory of factor proportion

Fatima Reply

What is inflation

Bright Reply

a general and ongoing rise in the level of prices in an economy

AI-Robot

What are the factors that affect demand for a commodity

Florence Reply

price

Kenu

Got questions? Join the online conversation and get instant answers!

Jobilize.com Reply

<< Chapter < Page Page > Chapter >>

Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Precalculus. OpenStax CNX. Jan 19, 2016 Download for free at https://legacy.cnx.org/content/col11667/1.6

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Precalculus' conversation and receive update notifications?

Ask

	11 Verbal By OpenStax Read Online Course
	9 Key concepts By OpenStax Read Online Course
	11 Biology 11 Meiosis Sexual Reproduction MCQ By OpenStax Start Quiz
	2 Microeconomics 02 Choice in a World of Scarcity By OpenStax Start Flashcards
	6 BOD Respiratory Exam By Brooke Delaney Start Exam
	13 Lec:13 Hypothesis Testing P-values By Janet Forrester Start Quiz
©flickr: U.S.	Biology Chapter 10 By Michael Sag Start Exam
	19 AP 19 Cardiovascular System Heart Essay By OpenStax Start Flashcards
	Anthropology Religion Culture By Richley Crapo Start Assignment
	Deciduous Forest By Hope Percle Start Quiz
	Worldport Outside By Rachel Carlisle Start Quiz
	Microeconomics Test 1 By IES Portal Start Test