| << Chapter < Page | Chapter >> Page > |
At the beginning of this section, we learned that the population of India was about billion in the year 2013, with an annual growth rate of about This situation is represented by the growth function where is the number of years since To the nearest thousandth, what will the population of India be in
To estimate the population in 2031, we evaluate the models for because 2031 is years after 2013. Rounding to the nearest thousandth,
There will be about 1.549 billion people in India in the year 2031.
The population of China was about 1.39 billion in the year 2013, with an annual growth rate of about This situation is represented by the growth function where is the number of years since To the nearest thousandth, what will the population of China be for the year 2031? How does this compare to the population prediction we made for India in [link] ?
About billion people; by the year 2031, India’s population will exceed China’s by about 0.001 billion, or 1 million people.
In the previous examples, we were given an exponential function, which we then evaluated for a given input. Sometimes we are given information about an exponential function without knowing the function explicitly. We must use the information to first write the form of the function, then determine the constants and and evaluate the function.
Given two data points, write an exponential model.
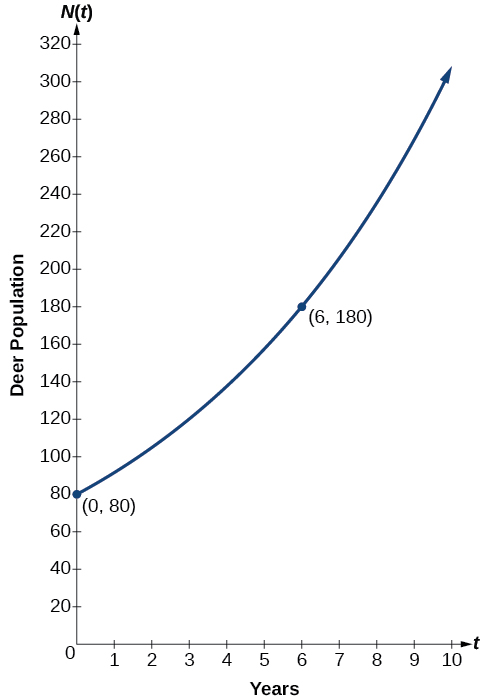
In 2006, 80 deer were introduced into a wildlife refuge. By 2012, the population had grown to 180 deer. The population was growing exponentially. Write an algebraic function representing the population of deer over time
We let our independent variable be the number of years after 2006. Thus, the information given in the problem can be written as input-output pairs: (0, 80) and (6, 180). Notice that by choosing our input variable to be measured as years after 2006, we have given ourselves the initial value for the function, We can now substitute the second point into the equation to find
NOTE: Unless otherwise stated, do not round any intermediate calculations. Then round the final answer to four places for the remainder of this section.
The exponential model for the population of deer is (Note that this exponential function models short-term growth. As the inputs gets large, the output will get increasingly larger, so much so that the model may not be useful in the long term.)
We can graph our model to observe the population growth of deer in the refuge over time. Notice that the graph in [link] passes through the initial points given in the problem, and We can also see that the domain for the function is and the range for the function is

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?