| << Chapter < Page | Chapter >> Page > |
Notice that the functions from previous examples were all polynomials, and their inverses were radical functions. If we want to find the inverse of a radical function , we will need to restrict the domain of the answer because the range of the original function is limited.
Given a radical function, find the inverse.
Restrict the domain and then find the inverse of the function
Note that the original function has range Replace with then solve for
Recall that the domain of this function must be limited to the range of the original function.
Restrict the domain and then find the inverse of the function
Radical functions are common in physical models, as we saw in the section opener. We now have enough tools to be able to solve the problem posed at the start of the section.
A mound of gravel is in the shape of a cone with the height equal to twice the radius. The volume of the cone in terms of the radius is given by
Find the inverse of the function that determines the volume of a cone and is a function of the radius Then use the inverse function to calculate the radius of such a mound of gravel measuring 100 cubic feet. Use
Start with the given function for
Notice that the meaningful domain for the function is
since negative radii would not make sense in this context. Also note the range of the function (hence, the domain of the inverse function) is
Solve for
in terms of
using the method outlined previously.
This is the result stated in the section opener. Now evaluate this for and
Therefore, the radius is about 3.63 ft.
When radical functions are composed with other functions, determining domain can become more complicated.
Find the domain of the function
Because a square root is only defined when the quantity under the radical is non-negative, we need to determine where The output of a rational function can change signs (change from positive to negative or vice versa) at x -intercepts and at vertical asymptotes. For this equation, the graph could change signs at = –2, 1, and 3.
To determine the intervals on which the rational expression is positive, we could test some values in the expression or sketch a graph. While both approaches work equally well, for this example we will use a graph as shown in [link] .
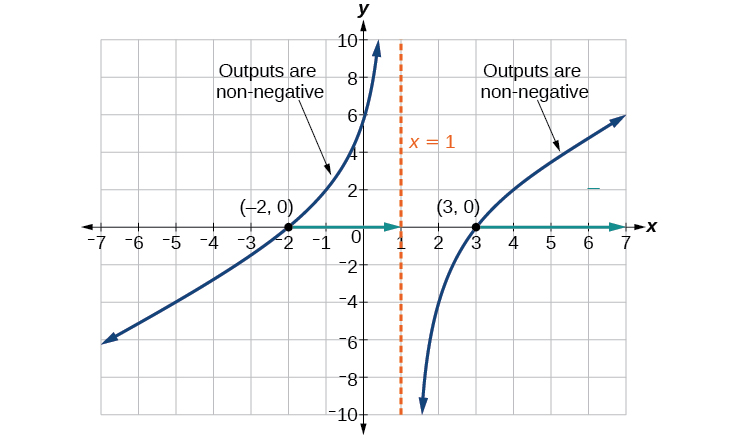
This function has two x -intercepts, both of which exhibit linear behavior near the x -intercepts. There is one vertical asymptote, corresponding to a linear factor; this behavior is similar to the basic reciprocal toolkit function, and there is no horizontal asymptote because the degree of the numerator is larger than the degree of the denominator. There is a y -intercept at
From the y -intercept and x -intercept at we can sketch the left side of the graph. From the behavior at the asymptote, we can sketch the right side of the graph.
From the graph, we can now tell on which intervals the outputs will be non-negative, so that we can be sure that the original function will be defined. has domain or in interval notation,

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?