5.3 Time dilation  (Page 5/8)

Solution

1. Identify the knowns (from part a):
   
   $\text{Δ}t=3.33\times {10}^{\mathrm{-9}}\text{s;}v=6.00\times {10}^7\text{m/s;}d=0.200\text{m.}$
2. Identify the unknown: $\tau .$
3. Express the answer as an equation:
   
   $\begin{array}{ccc}\hfill \text{Δ}t& =\hfill & \gamma \text{Δ}\tau =\frac{\text{Δ}\tau }{\sqrt{1-v^2\text{/}{c}^2}}\hfill \\ \hfill \text{Δ}\tau & =\hfill & \text{Δ}t\sqrt{1-v^2\text{/}{c}^2}.\hfill \end{array}$
4. Do the calculation:
   
   $\begin{array}{cc}\hfill \text{Δ}\tau & =\left(3.33\times {10}^{\mathrm{-9}}\text{s}\right)\sqrt{1-{\left(\frac{6.00\times {10}^7\text{m/s}}{3.00\times {10}^8\text{m/s}}\right)}^2}\hfill \\ & =3.26\times {10}^{\mathrm{-9}}\text{s.}\hfill \end{array}$

Significance

The twin paradox

An intriguing consequence of time dilation is that a space traveler moving at a high velocity relative to Earth would age less than the astronaut’s earthbound twin. This is often known as the twin paradox . Imagine the astronaut moving at such a velocity that $\gamma =30.0,$ as in [link] . A trip that takes 2.00 years in her frame would take 60.0 years in the earthbound twin’s frame. Suppose the astronaut travels 1.00 year to another star system, briefly explores the area, and then travels 1.00 year back. An astronaut who was 40 years old at the start of the trip would be would be 42 when the spaceship returns. Everything on Earth, however, would have aged 60.0 years. The earthbound twin, if still alive, would be 100 years old.

The situation would seem different to the astronaut in [link] . Because motion is relative, the spaceship would seem to be stationary and Earth would appear to move. (This is the sensation you have when flying in a jet.) Looking out the window of the spaceship, the astronaut would see time slow down on Earth by a factor of $\gamma =30.0.$ Seen from the spaceship, the earthbound sibling will have aged only 2/30, or 0.07, of a year, whereas the astronaut would have aged 2.00 years.

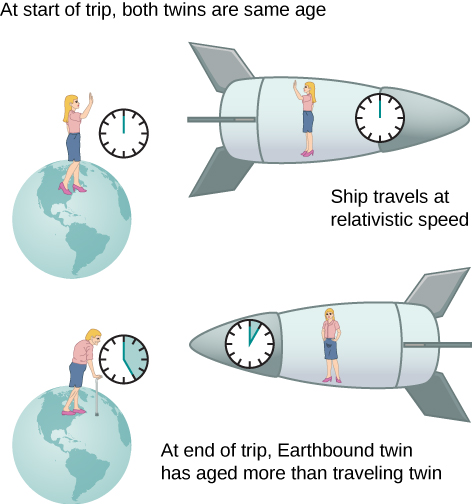
The paradox here is that the two twins cannot both be correct. As with all paradoxes, conflicting conclusions come from a false premise. In fact, the astronaut’s motion is significantly different from that of the earthbound twin. The astronaut accelerates to a high velocity and then decelerates to view the star system. To return to Earth, she again accelerates and decelerates. The spacecraft is not in a single inertial frame to which the time dilation formula can be directly applied. That is, the astronaut twin changes inertial references. The earthbound twin does not experience these accelerations and remains in the same inertial frame. Thus, the situation is not symmetric, and it is incorrect to claim that the astronaut observes the same effects as her twin. The lack of symmetry between the twins will be still more evident when we analyze the journey later in this chapter in terms of the path the astronaut follows through four-dimensional space-time.