| << Chapter < Page | Chapter >> Page > |
Check Your Understanding What does the energy separation between absorption lines in a rotational spectrum of a diatomic molecule tell you?
the moment of inertia
The vibrational energy level , which is the energy level associated with the vibrational energy of a molecule, is more difficult to estimate than the rotational energy level. However, we can estimate these levels by assuming that the two atoms in the diatomic molecule are connected by an ideal spring of spring constant k . The potential energy of this spring system is
Where is a change in the “natural length” of the molecule along a line that connects the atoms. Solving Schrödinger’s equation for this potential gives
Where is the natural angular frequency of vibration and n is the vibrational quantum number. The prediction that vibrational energy levels are evenly spaced turns out to be good at lower energies.
A detailed study of transitions between vibrational energy levels induced by the absorption or emission of radiation (and the specifically so-called electric dipole transition) requires that
[link] represents the selection rule for vibrational energy transitions. As mentioned before, this rule applies only to diatomic molecules that have an electric dipole moment. Symmetric molecules do not experience such transitions.
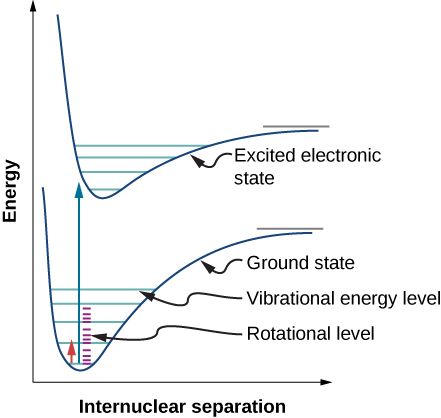
Due to the selection rules, the absorption or emission of radiation by a diatomic molecule involves a transition in vibrational and rotational states. Specifically, if the vibrational quantum number ( n ) changes by one unit, then the rotational quantum number ( l ) changes by one unit. An energy-level diagram of a possible transition is given in [link] . The absorption spectrum for such transitions in hydrogen chloride (HCl) is shown in [link] . The absorption peaks are due to transitions from the to vibrational states. Energy differences for the band of peaks at the left and right are, respectively, and
The moment of inertia can then be determined from the energy spacing between individual peaks or from the gap between the left and right bands . The frequency at the center of this gap is the frequency of vibration.
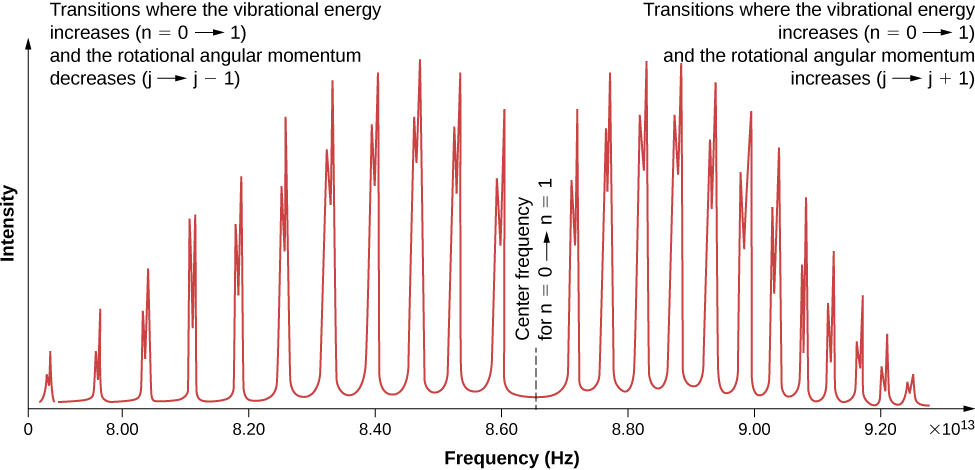
Does the absorption spectrum of the diatomic molecule HCl depend on the isotope of chlorine contained in the molecule? Explain your reasoning.
Rank the energy spacing of the following transitions from least to greatest: an electron energy transition in an atom (atomic energy), the rotational energy of a molecule, or the vibrational energy of a molecule?
rotational energy, vibrational energy, and atomic energy
Explain key features of a vibrational-rotation energy spectrum of the diatomic molecule.
In a physics lab, you measure the vibrational-rotational spectrum of HCl. The estimated separation between absorption peaks is . The central frequency of the band is . (a) What is the moment of inertia ( I )? (b) What is the energy of vibration for the molecule?
For the preceding problem, find the equilibrium separation of the H and Cl atoms. Compare this with the actual value.
The measured value is 0.484 nm, and the actual value is close to 0.127 nm. The laboratory results are the same order of magnitude, but a factor 4 high.
The separation between oxygen atoms in an molecule is about 0.121 nm. Determine the characteristic energy of rotation in eV.
The characteristic energy of the molecule is . Determine the separation distance between the nitrogen atoms
0.110 nm
The characteristic energy for KCl is (a) Determine for the KCl molecule. (b) Find the separation distance between the K and Cl atoms.
A diatomic molecule is in the state. (a) What is the energy of the molecule? (b) How much energy is radiated in a transition from a to a state?
a. ; b.
In a physics lab, you measure the vibrational-rotational spectrum of potassium bromide (KBr). The estimated separation between absorption peaks is . The central frequency of the band is . (a) What is the moment of inertia ( I )? (b) What is the energy of vibration for the molecule?

Notification Switch
Would you like to follow the 'University physics volume 3' conversation and receive update notifications?