| << Chapter < Page | Chapter >> Page > |
The law of refraction can be explained by applying Huygens’s principle to a wave front passing from one medium to another ( [link] ). Each wavelet in the figure was emitted when the wave front crossed the interface between the media. Since the speed of light is smaller in the second medium, the waves do not travel as far in a given time, and the new wave front changes direction as shown. This explains why a ray changes direction to become closer to the perpendicular when light slows down. Snell’s law can be derived from the geometry in [link] ( [link] ).
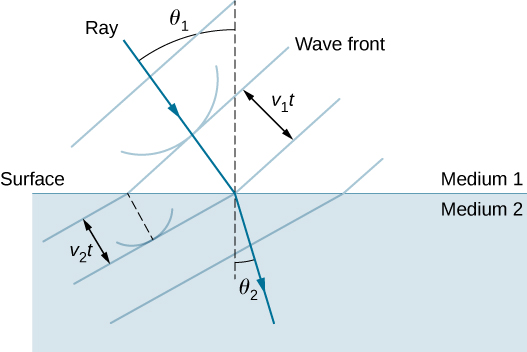
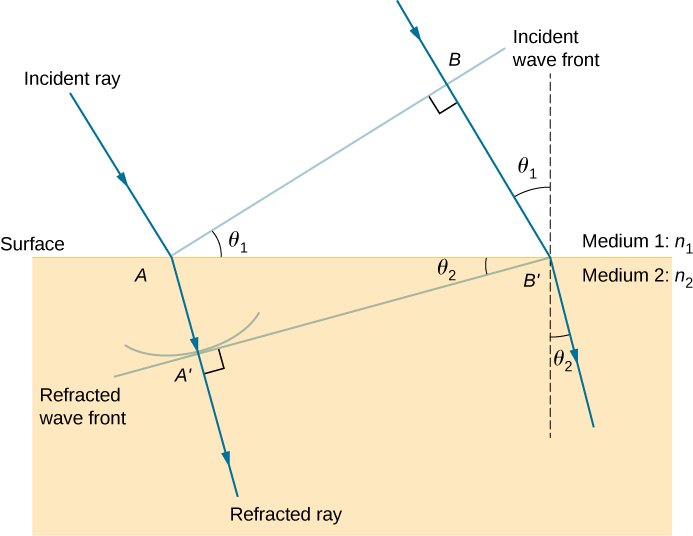
The length of is given in two ways as
Inverting the equation and substituting from above and similarly , we obtain
Cancellation of allows us to simplify this equation into the familiar form
Check Your Understanding In [link] , we had . If were decreased such that and the speed of light in medium 2 is faster than in medium 1, what would happen to the length of ? What would happen to the wave front and the direction of the refracted ray?
becomes longer, tilts further away from the surface, and the refracted ray tilts away from the normal.
This applet by Walter Fendt shows an animation of reflection and refraction using Huygens’s wavelets while you control the parameters. Be sure to click on “Next step” to display the wavelets. You can see the reflected and refracted wave fronts forming.
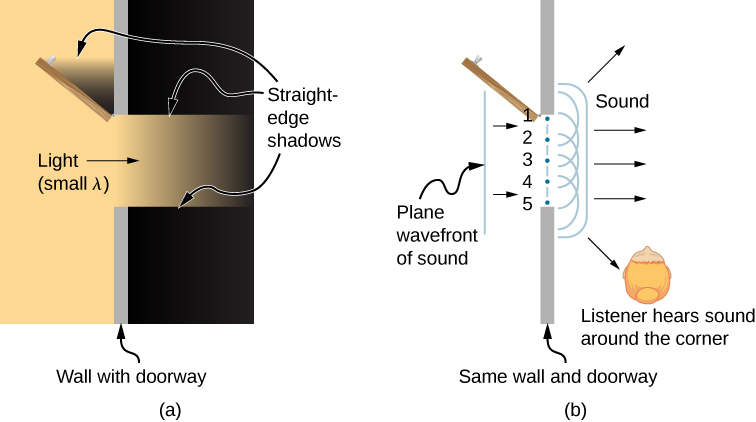
What happens when a wave passes through an opening, such as light shining through an open door into a dark room? For light, we observe a sharp shadow of the doorway on the floor of the room, and no visible light bends around corners into other parts of the room. When sound passes through a door, we hear it everywhere in the room and thus observe that sound spreads out when passing through such an opening ( [link] ). What is the difference between the behavior of sound waves and light waves in this case? The answer is that light has very short wavelengths and acts like a ray. Sound has wavelengths on the order of the size of the door and bends around corners (for frequency of 1000 Hz,
about three times smaller than the width of the doorway).
If we pass light through smaller openings such as slits, we can use Huygens’s principle to see that light bends as sound does ( [link] ). The bending of a wave around the edges of an opening or an obstacle is called diffraction. Diffraction is a wave characteristic and occurs for all types of waves. If diffraction is observed for some phenomenon, it is evidence that the phenomenon is a wave. Thus, the horizontal diffraction of the laser beam after it passes through the slits in [link] is evidence that light is a wave. You will learn about diffraction in much more detail in the chapter on Diffraction .
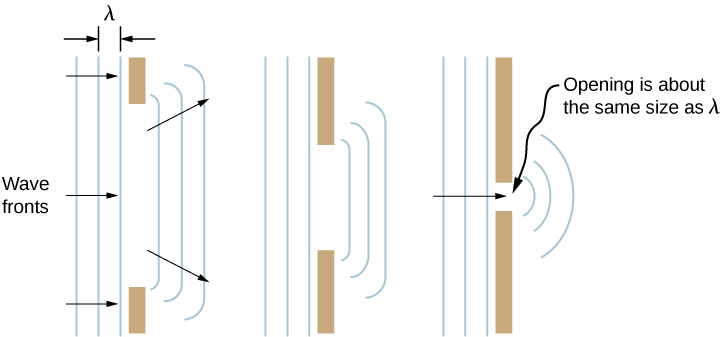
How do wave effects depend on the size of the object with which the wave interacts? For example, why does sound bend around the corner of a building while light does not?
If diffraction is observed for some phenomenon, it is evidence that the phenomenon is a wave. Does the reverse hold true? That is, if diffraction is not observed, does that mean the phenomenon is not a wave?

Notification Switch
Would you like to follow the 'University physics volume 3' conversation and receive update notifications?