10.2 Nuclear binding energy  (Page 2/5)

Graph of binding energy per nucleon

In nuclear physics, one of the most important experimental quantities is the binding energy per nucleon (BEN)    , which is defined by

This quantity is the average energy required to remove an individual nucleon from a nucleus—analogous to the ionization energy of an electron in an atom. If the BEN is relatively large, the nucleus is relatively stable. BEN values are estimated from nuclear scattering experiments.

A graph of binding energy per nucleon versus atomic number A is given in [link] . This graph is considered by many physicists to be one of the most important graphs in physics. Two notes are in order. First, typical BEN values range from 6–10 MeV, with an average value of about 8 MeV. In other words, it takes several million electron volts to pry a nucleon from a typical nucleus, as compared to just 13.6 eV to ionize an electron in the ground state of hydrogen. This is why nuclear force is referred to as the “strong” nuclear force.

Second, the graph rises at low A , peaks very near iron $\left(\text{Fe},A=56\right),$ and then tapers off at high A . The peak value suggests that the iron nucleus is the most stable nucleus in nature (it is also why nuclear fusion in the cores of stars ends with Fe). The reason the graph rises and tapers off has to do with competing forces in the nucleus. At low values of A , attractive nuclear forces between nucleons dominate over repulsive electrostatic forces between protons. But at high values of A , repulsive electrostatic forces between forces begin to dominate, and these forces tend to break apart the nucleus rather than hold it together.

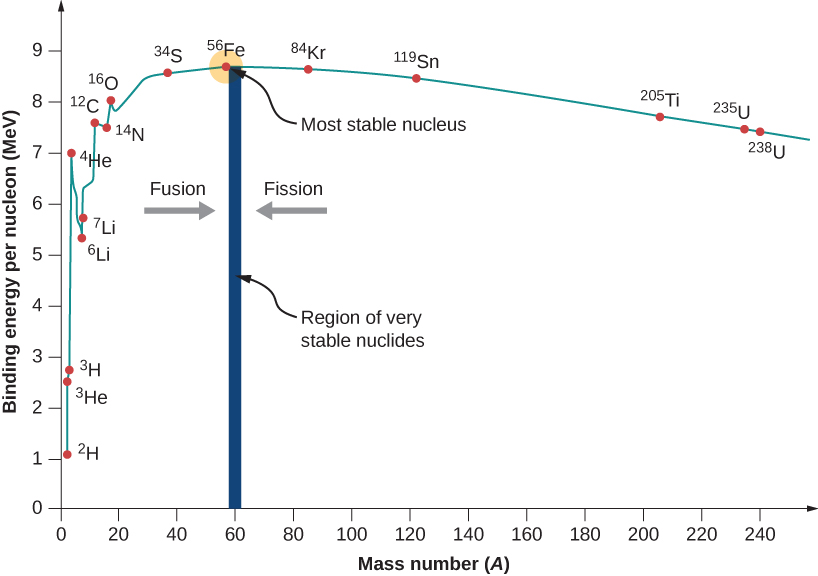
As we will see, the BEN-versus- A graph implies that nuclei divided or combined release an enormous amount of energy. This is the basis for a wide range of phenomena, from the production of electricity at a nuclear power plant to sunlight.

Summary

• The mass defect of a nucleus is the difference between the total mass of a nucleus and the sum of the masses of all its constituent nucleons.
• The binding energy (BE) of a nucleus is equal to the amount of energy released in forming the nucleus, or the mass defect multiplied by the speed of light squared.
• A graph of binding energy per nucleon (BEN) versus atomic number A implies that nuclei divided or combined release an enormous amount of energy.
• The binding energy of a nucleon in a nucleus is analogous to the ionization energy of an electron in an atom.

Conceptual questions

Problems