7.3 The schrӧdinger equation  (Page 2/5)

Consider the special case of a free particle. A free particle experiences no force $(F=0).$ Based on [link] , this requires only that

For simplicity, we set $U_0=0$ . Schrӧdinger’s equation then reduces to

A valid solution to this equation is

Not surprisingly, this solution contains an imaginary number $(i=\sqrt{\mathrm{-1}})$ because the differential equation itself contains an imaginary number. As stressed before, however, quantum-mechanical predictions depend only on ${\left|\text{Ψ}\left(x,t\right)\right|}^2$ , which yields completely real values. Notice that the real plane-wave solutions, $\text{Ψ}\left(x,t\right)=A\text{sin}\left(kx-\omega t\right)$ and $\text{Ψ}\left(x,t\right)=A\text{cos}\left(kx-\omega t\right),$ do not obey Schrödinger’s equation. The temptation to think that a wave function can be seen, touched, and felt in nature is eliminated by the appearance of an imaginary number. In Schrӧdinger’s theory of quantum mechanics, the wave function is merely a tool for calculating things.

If the potential energy function ( U ) does not depend on time, it is possible to show that

satisfies Schrӧdinger’s time-dependent equation, where $\psi \left(x\right)$ is a time -independent function and $e^{\text{−}i\omega t}$ is a space -independent function. In other words, the wave function is separable into two parts: a space-only part and a time-only part. The factor $e^{\text{−}i\omega t}$ is sometimes referred to as a time-modulation factor    since it modifies the space-only function. According to de Broglie, the energy of a matter wave is given by $E=\hslash \omega$ , where E is its total energy. Thus, the above equation can also be written as

Any linear combination of such states (mixed state of energy or momentum) is also valid solution to this equation. Such states can, for example, describe a localized particle (see [link] )

Combining [link] and [link] , Schrödinger’s time-dependent equation reduces to

where E is the total energy of the particle (a real number). This equation is called Schrӧdinger’s time-independent equation    . Notice that we use “big psi” $(\text{Ψ})$ for the time-dependent wave function and “little psi” $(\psi )$ for the time-independent wave function. The wave-function solution to this equation must be multiplied by the time-modulation factor to obtain the time-dependent wave function.

In the next sections, we solve Schrӧdinger’s time-independent equation for three cases: a quantum particle in a box, a simple harmonic oscillator, and a quantum barrier. These cases provide important lessons that can be used to solve more complicated systems. The time-independent wave function $\psi \left(x\right)$ solutions must satisfy three conditions:

• $\psi \left(x\right)$ must be a continuous function.
• The first derivative of $\psi \left(x\right)$ with respect to space, $d\psi \left(x\right)\text{/}dx$ , must be continuous, unless $V\left(x\right)=\infty$ .
• $\psi \left(x\right)$ must not diverge (“blow up”) at $x=\text{±}\infty .$

The first condition avoids sudden jumps or gaps in the wave function. The second condition requires the wave function to be smooth at all points, except in special cases. (In a more advanced course on quantum mechanics, for example, potential spikes of infinite depth and height are used to model solids). The third condition requires the wave function be normalizable. This third condition follows from Born’s interpretation of quantum mechanics. It ensures that ${\left|\psi \left(x\right)\right|}^2$ is a finite number so we can use it to calculate probabilities.

Check Your Understanding Which of the following wave functions is a valid wave-function solution for Schrӧdinger’s equation?

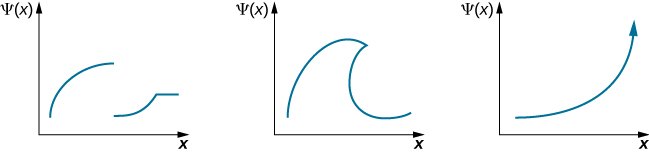
None. The first function has a discontinuity; the second function is double-valued; and the third function diverges so is not normalizable.

Got questions? Get instant answers now!

Summary

• The Schrӧdinger equation is the fundamental equation of wave quantum mechanics. It allows us to make predictions about wave functions.
• When a particle moves in a time-independent potential, a solution of the time-dependent Schrӧdinger equation is a product of a time-independent wave function and a time-modulation factor.
• The Schrӧdinger equation can be applied to many physical situations.

Conceptual questions

Problems