| << Chapter < Page | Chapter >> Page > |
A light ray that strikes an object consisting of two mutually perpendicular reflecting surfaces is reflected back exactly parallel to the direction from which it came ( [link] ). This is true whenever the reflecting surfaces are perpendicular, and it is independent of the angle of incidence. (For proof, see [link] at the end of this section.) Such an object is called a corner reflector , since the light bounces from its inside corner. Corner reflectors are a subclass of retroreflectors, which all reflect rays back in the directions from which they came. Although the geometry of the proof is much more complex, corner reflectors can also be built with three mutually perpendicular reflecting surfaces and are useful in three-dimensional applications.
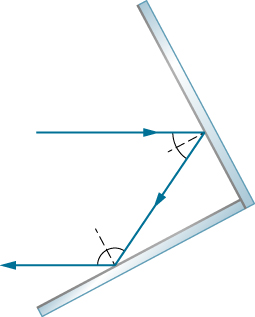
Many inexpensive reflector buttons on bicycles, cars, and warning signs have corner reflectors designed to return light in the direction from which it originated. Rather than simply reflecting light over a wide angle, retroreflection ensures high visibility if the observer and the light source are located together, such as a car’s driver and headlights. The Apollo astronauts placed a true corner reflector on the Moon ( [link] ). Laser signals from Earth can be bounced from that corner reflector to measure the gradually increasing distance to the Moon of a few centimeters per year.

Working on the same principle as these optical reflectors, corner reflectors are routinely used as radar reflectors ( [link] ) for radio-frequency applications. Under most circumstances, small boats made of fiberglass or wood do not strongly reflect radio waves emitted by radar systems. To make these boats visible to radar (to avoid collisions, for example), radar reflectors are attached to boats, usually in high places.

As a counterexample, if you are interested in building a stealth airplane, radar reflections should be minimized to evade detection. One of the design considerations would then be to avoid building corners into the airframe.
Using the law of reflection, explain how powder takes the shine off of a person’s nose. What is the name of the optical effect?
Powder consists of many small particles with randomly oriented surfaces. This leads to diffuse reflection, reducing shine.
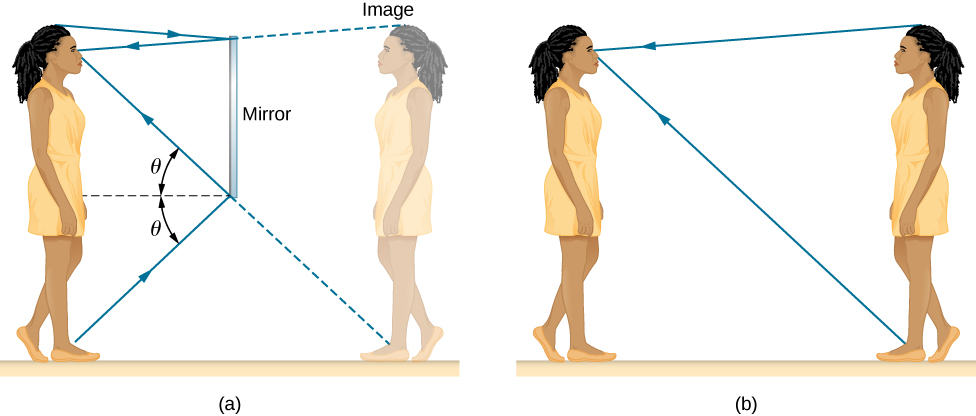
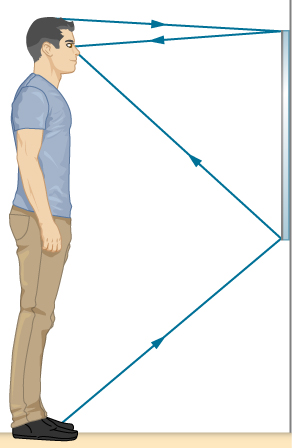
Suppose a man stands in front of a mirror as shown below. His eyes are 1.65 m above the floor and the top of his head is 0.13 m higher. Find the height above the floor of the top and bottom of the smallest mirror in which he can see both the top of his head and his feet. How is this distance related to the man’s height?
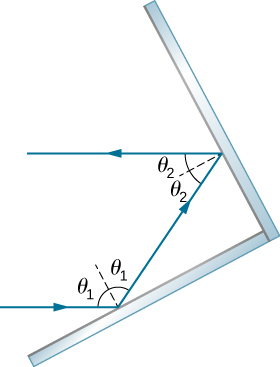
Show that when light reflects from two mirrors that meet each other at a right angle, the outgoing ray is parallel to the incoming ray, as illustrated below.
proof
On the Moon’s surface, lunar astronauts placed a corner reflector, off which a laser beam is periodically reflected. The distance to the Moon is calculated from the round-trip time. What percent correction is needed to account for the delay in time due to the slowing of light in Earth’s atmosphere? Assume the distance to the Moon is precisely and Earth’s atmosphere (which varies in density with altitude) is equivalent to a layer 30.0 km thick with a constant index of refraction
A flat mirror is neither converging nor diverging. To prove this, consider two rays originating from the same point and diverging at an angle (see below). Show that after striking a plane mirror, the angle between their directions remains
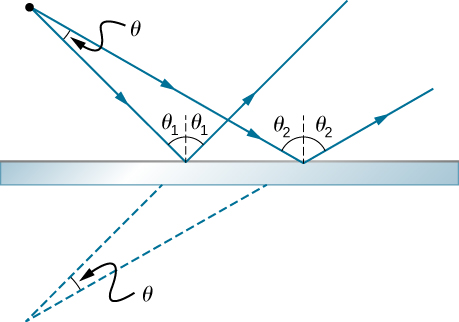
proof

Notification Switch
Would you like to follow the 'University physics volume 3' conversation and receive update notifications?