9.6 Semiconductors and doping  (Page 3/14)

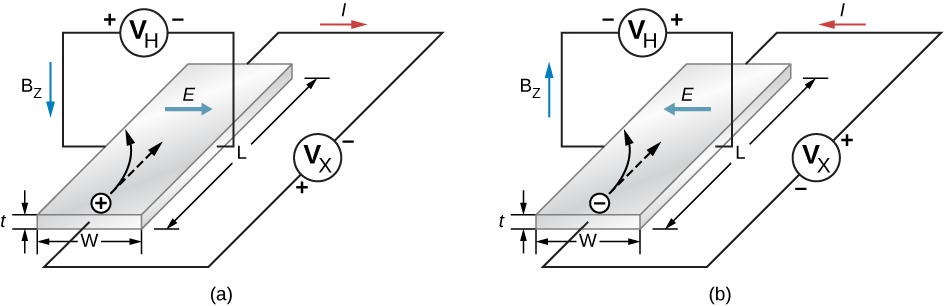
where $V_{\text{H}}$ is the Hall voltage; v is the hole’s drift velocity    , or average velocity of a particle that moves in a partially random fashion; B is the magnetic field strength; and w is the width of the strip. Note that the Hall voltage is transverse to the voltage that initially produces current through the material. A measurement of the sign of this voltage (or potential difference) confirms the collection of holes on the top side of the strip. The magnitude of the Hall voltage yields the drift velocity ( v ) of the majority carriers.

Additional information can also be extracted from the Hall voltage. Note that the electron current density (the amount of current per unit cross-sectional area of the semiconductor strip) is

where q is the magnitude of the charge, n is the number of charge carriers per unit volume, and v is the drift velocity. The current density is easily determined by dividing the total current by the cross-sectional area of the strip, q is charge of the hole (the magnitude of the charge of a single electron), and u is determined by the Hall effect [link] . Hence, the above expression for the electron current density gives the number of charge carriers per unit volume, n . A similar analysis can be conducted for negatively charged carriers in an n -type material (see [link] ).

Summary

• The energy structure of a semiconductor can be altered by substituting one type of atom with another (doping).
• Semiconductor n -type doping creates and fills new energy levels just below the conduction band.
• Semiconductor p -type doping creates new energy levels just above the valence band.
• The Hall effect can be used to determine charge, drift velocity, and charge carrier number density of a semiconductor.

Conceptual questions

Problems