6.1 Blackbody radiation  (Page 5/15)

In [link] , f is the frequency of Planck’s oscillator. The natural number n that enumerates these discrete energies is called a quantum number . The physical constant h is called Planck’s constant :

Each discrete energy value corresponds to a quantum state of a Planck oscillator . Quantum states are enumerated by quantum numbers. For example, when Planck’s oscillator is in its first $n=1$ quantum state, its energy is $E_1=hf;$ when it is in the $n=2$ quantum state, its energy is $E_2=2hf;$ when it is in the $n=3$ quantum state, $E_3=3hf;$ and so on.

Note that [link] shows that there are infinitely many quantum states, which can be represented as a sequence { hf , 2 hf , 3 hf ,…, ( n – 1) hf , nhf , ( n + 1) hf ,…}. Each two consecutive quantum states in this sequence are separated by an energy jump, $\text{Δ}E=hf.$ An oscillator in the wall can receive energy from the radiation in the cavity (absorption), or it can give away energy to the radiation in the cavity (emission). The absorption process sends the oscillator to a higher quantum state, and the emission process sends the oscillator to a lower quantum state. Whichever way this exchange of energy goes, the smallest amount of energy that can be exchanged is hf . There is no upper limit to how much energy can be exchanged, but whatever is exchanged must be an integer multiple of hf . If the energy packet does not have this exact amount, it is neither absorbed nor emitted at the wall of the blackbody.

Recall that the frequency of electromagnetic radiation is related to its wavelength and to the speed of light by the fundamental relation $f\lambda =c.$ This means that we can express [link] equivalently in terms of wavelength $\lambda .$ When included in the computation of the energy density of a blackbody, Planck’s hypothesis gives the following theoretical expression for the power intensity of emitted radiation per unit wavelength:

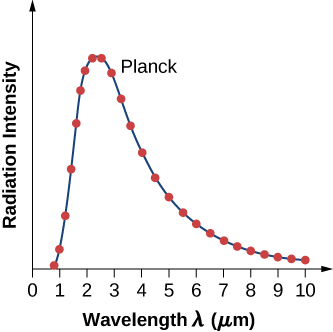
where c is the speed of light in vacuum and $k_{\text{B}}$ is Boltzmann’s constant, $k_{\text{B}}=1.380\times {10}^{\mathrm{-23}}\text{J/K}.$ The theoretical formula expressed in [link] is called Planck’s blackbody radiation law . This law is in agreement with the experimental blackbody radiation curve (see [link] ). In addition, Wien’s displacement law and Stefan’s law can both be derived from [link] . To derive Wien’s displacement law, we use differential calculus to find the maximum of the radiation intensity curve $I(\lambda ,T).$ To derive Stefan’s law and find the value of the Stefan–Boltzmann constant, we use integral calculus and integrate $I(\lambda ,T)$ to find the total power radiated by a blackbody at one temperature in the entire spectrum of wavelengths from $\lambda =0$ to $\lambda =\infty .$ This derivation is left as an exercise later in this chapter.