| << Chapter < Page | Chapter >> Page > |
The term “blackbody” was coined by Gustav R. Kirchhoff in 1862. The blackbody radiation curve was known experimentally, but its shape eluded physical explanation until the year 1900. The physical model of a blackbody at temperature T is that of the electromagnetic waves enclosed in a cavity (see [link] ) and at thermodynamic equilibrium with the cavity walls. The waves can exchange energy with the walls. The objective here is to find the energy density distribution among various modes of vibration at various wavelengths (or frequencies). In other words, we want to know how much energy is carried by a single wavelength or a band of wavelengths. Once we know the energy distribution, we can use standard statistical methods (similar to those studied in a previous chapter) to obtain the blackbody radiation curve, Stefan’s law, and Wien’s displacement law. When the physical model is correct, the theoretical predictions should be the same as the experimental curves.
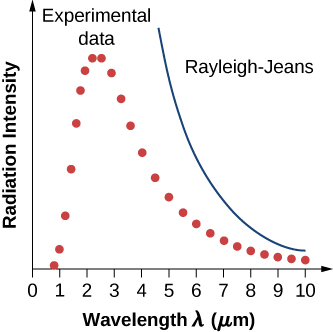
In a classical approach to the blackbody radiation problem, in which radiation is treated as waves (as you have studied in previous chapters), the modes of electromagnetic waves trapped in the cavity are in equilibrium and continually exchange their energies with the cavity walls. There is no physical reason why a wave should do otherwise: Any amount of energy can be exchanged, either by being transferred from the wave to the material in the wall or by being received by the wave from the material in the wall. This classical picture is the basis of the model developed by Lord Rayleigh and, independently, by Sir James Jeans. The result of this classical model for blackbody radiation curves is known as the Rayleigh–Jeans law . However, as shown in [link] , the Rayleigh–Jeans law fails to correctly reproduce experimental results. In the limit of short wavelengths, the Rayleigh–Jeans law predicts infinite radiation intensity, which is inconsistent with the experimental results in which radiation intensity has finite values in the ultraviolet region of the spectrum. This divergence between the results of classical theory and experiments, which came to be called the ultraviolet catastrophe , shows how classical physics fails to explain the mechanism of blackbody radiation.
The blackbody radiation problem was solved in 1900 by Max Planck . Planck used the same idea as the Rayleigh–Jeans model in the sense that he treated the electromagnetic waves between the walls inside the cavity classically, and assumed that the radiation is in equilibrium with the cavity walls. The innovative idea that Planck introduced in his model is the assumption that the cavity radiation originates from atomic oscillations inside the cavity walls, and that these oscillations can have only discrete values of energy. Therefore, the radiation trapped inside the cavity walls can exchange energy with the walls only in discrete amounts. Planck’s hypothesis of discrete energy values, which he called quanta , assumes that the oscillators inside the cavity walls have quantized energies . This was a brand new idea that went beyond the classical physics of the nineteenth century because, as you learned in a previous chapter, in the classical picture, the energy of an oscillator can take on any continuous value. Planck assumed that the energy of an oscillator ( ) can have only discrete, or quantized, values:

Notification Switch
Would you like to follow the 'University physics volume 3' conversation and receive update notifications?