| << Chapter < Page | Chapter >> Page > |
| Material | Index of Refraction |
|---|---|
| Water | 1.33 |
| Air | 1.0 |
| Cornea | 1.38 |
| Aqueous humor | 1.34 |
| Lens | 1.41 * |
| Vitreous humor | 1.34 |
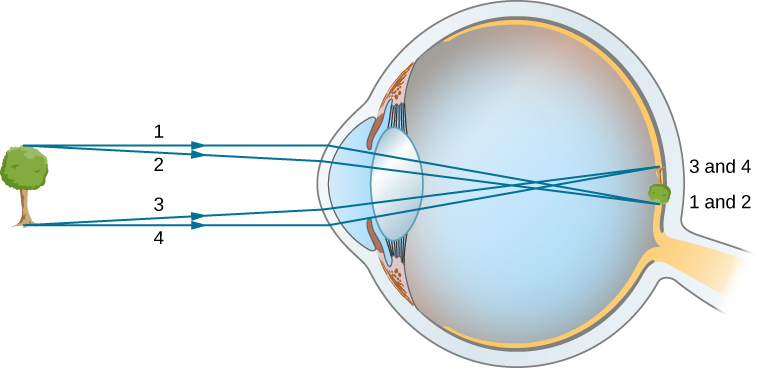
As noted, the image must fall precisely on the retina to produce clear vision—that is, the image distance must equal the lens-to-retina distance. Because the lens-to-retina distance does not change, the image distance must be the same for objects at all distances. The ciliary muscles adjust the shape of the eye lens for focusing on nearby or far objects. By changing the shape of the eye lens, the eye changes the focal length of the lens. This mechanism of the eye is called accommodation .
The nearest point an object can be placed so that the eye can form a clear image on the retina is called the near point of the eye. Similarly, the far point is the farthest distance at which an object is clearly visible. A person with normal vision can see objects clearly at distances ranging from 25 cm to essentially infinity. The near point increases with age, becoming several meters for some older people. In this text, we consider the near point to be 25 cm.
We can use the thin-lens equations to quantitatively examine image formation by the eye. First, we define the optical power of a lens as
with the focal length f given in meters. The units of optical power are called “diopters” (D). That is, . Optometrists prescribe common eyeglasses and contact lenses in units of diopters . With this definition of optical power, we can rewrite the thin-lens equations as
Working with optical power is convenient because, for two or more lenses close together, the effective optical power of the lens system is approximately the sum of the optical power of the individual lenses:
Hence, the focal length of the eye (cornea and lens together) is
The optical power of the eye is
For clear vision, the image distance must equal the lens-to-retina distance. Normal vision is possible for objects at distances to infinity. The following example shows how to calculate the image distance for an object placed at the near point of the eye.
Therefore, the image is formed 1.8 cm behind the lens.

Notification Switch
Would you like to follow the 'University physics volume 3' conversation and receive update notifications?