1. Home
  2. University physics volume 3
  3. Unit 1. optics
  4. The nature of light
  5. Huygens’s principle

1.6 Huygens’s principle  (Page 2/4)

<< Chapter < Page
  University physics volume 3     Page 2 / 4
Chapter >> Page >

Refraction

The law of refraction can be explained by applying Huygens’s principle to a wave front passing from one medium to another ( [link] ). Each wavelet in the figure was emitted when the wave front crossed the interface between the media. Since the speed of light is smaller in the second medium, the waves do not travel as far in a given time, and the new wave front changes direction as shown. This explains why a ray changes direction to become closer to the perpendicular when light slows down. Snell’s law can be derived from the geometry in [link] ( [link] ).

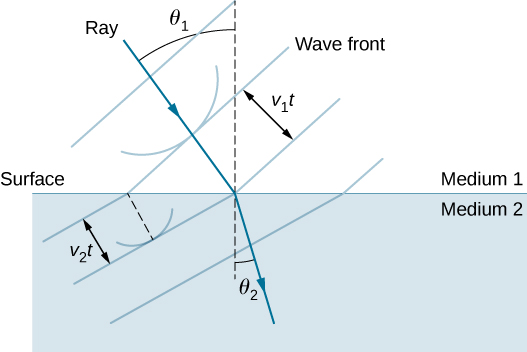
The figure shows two media separated by a horizontal line labeled surface. The upper medium is labeled medium one and the lower medium is labeled medium two. In medium one, a ray is incident on the surface, traveling down and to the right. A vertical dotted line, perpendicular to the surface, is drawn through both media where the ray hits the surface. The refracted ray bends down, toward this dotted line where it enters medium two. The path of the ray makes an angle theta sub one with the dotted line in medium one and an angle theta sub two with the dotted line in medium two, where theta sub two is less than theta sub one. Line segments, labeled wave front, are drawn perpendicular to the incident ray and the refracted ray. These line segments are equally spaced within each medium, but the three line segments in medium 1 are more widely spaced than the three line segments in medium 2. The separation of these line segments in medium 1 is labeled v sub one t and the separation in medium 2 is labeled v sub two t, with v sub two t being less than v sub one t.
Huygens’s principle applied to a plane wave front traveling from one medium to another, where its speed is less. The ray bends toward the perpendicular, since the wavelets have a lower speed in the second medium.

Deriving the law of refraction

By examining the geometry of the wave fronts, derive the law of refraction.

Strategy

Consider [link] , which expands upon [link] . It shows the incident wave front just reaching the surface at point A , while point B is still well within medium 1. In the time Δ t it takes for a wavelet from B to reach B ′ on the surface at speed v 1 = c / n 1 , a wavelet from A travels into medium 2 a distance of A A ′ = v 2 Δ t , where v 2 = c / n 2 . Note that in this example, v 2 is slower than v 1 because n 1 < n 2 .

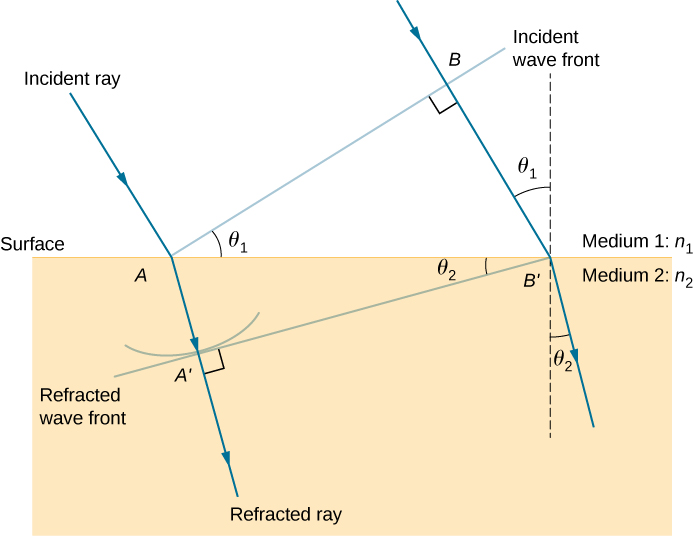
This figure illustrates the geometry of the refraction of the rays and wave fronts. A horizontal surface is present between medium 1, with index of refraction n 1, and medium 2, with index of refraction n 2. An incident ray is shown coming in from medium 1 into medium 2. It hits the surface at point A and refracts toward the normal in medium 2. A line, labeled incident wave front, is drawn from point A extending away from the surface, perpendicular to the incident ray. The angle between the incident wave front and the surface is theta 1. A second incident ray is drawn parallel to the first one. This ray intersects the incident wave front at a point labeled as B and hits the surface at a point labeled as B prime. A dashed line is drawn perpendicular to the surface at B prime. The angle between this perpendicular line and the second ray is also theta one. The triangle formed by A, B, and B prime is a right triangle with angle theta one at A and a right angle at B. The refracted rays at A and B prime bend down, toward the downward perpendiculars to the surface, making an angle of theta two with the vertical direction. The refracted wave front that is perpendicular to the refracted rays and that hits the surface at B prime is drawn. This wave front hits the refraction of the first incident ray at a point marked A prime and makes an angle of theta two with the surface.
Geometry of the law of refraction from medium 1 to medium 2.

Solution

The segment on the surface A B ′ is shared by both the triangle A B B ′ inside medium 1 and the triangle A A ′ B ′ inside medium 2. Note that from the geometry, the angle ∠ B A B ′ is equal to the angle of incidence, θ 1 . Similarly, ∠ A B ′ A ′ is θ 2 .

The length of A B ′ is given in two ways as

A B ′ = B B ′ sin θ 1 = A A ′ sin θ 2 .

Inverting the equation and substituting A A ′ = c Δ t / n 2 from above and similarly B B ′ = c Δ t / n 1 , we obtain

sin θ 1 c Δ t / n 1 = sin θ 2 c Δ t / n 2 .

Cancellation of c Δ t allows us to simplify this equation into the familiar form

n 1 sin θ 1 = n 2 sin θ 2 .

Significance

Although the law of refraction was established experimentally by Snell and stated in Refraction , its derivation here requires Huygens’s principle and the understanding that the speed of light is different in different media.

Got questions? Get instant answers now!

Check Your Understanding In [link] , we had n 1 < n 2 . If n 2 were decreased such that n 1 > n 2 and the speed of light in medium 2 is faster than in medium 1, what would happen to the length of A A ′ ? What would happen to the wave front A ′ B ′ and the direction of the refracted ray?

A A ′ becomes longer, A ′ B ′ tilts further away from the surface, and the refracted ray tilts away from the normal.

Got questions? Get instant answers now!

This applet by Walter Fendt shows an animation of reflection and refraction using Huygens’s wavelets while you control the parameters. Be sure to click on “Next step” to display the wavelets. You can see the reflected and refracted wave fronts forming.

Diffraction

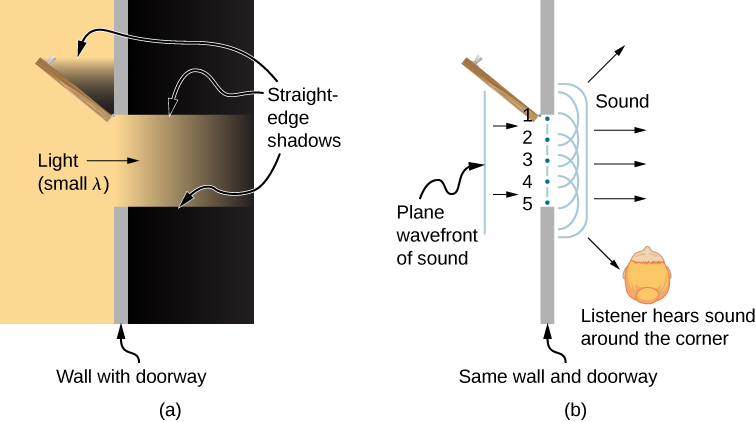
What happens when a wave passes through an opening, such as light shining through an open door into a dark room? For light, we observe a sharp shadow of the doorway on the floor of the room, and no visible light bends around corners into other parts of the room. When sound passes through a door, we hear it everywhere in the room and thus observe that sound spreads out when passing through such an opening ( [link] ). What is the difference between the behavior of sound waves and light waves in this case? The answer is that light has very short wavelengths and acts like a ray. Sound has wavelengths on the order of the size of the door and bends around corners (for frequency of 1000 Hz,

λ = c f = 330 m/s 1000 s −1 = 0.33 m,

about three times smaller than the width of the doorway).

Figure a is a view from above of a diagram of a wall in which there is an open doorway. The wall extends from the bottom of the diagram to the top, and the doorway forms a gap in the wall. The door itself is opened to the left and is positioned about forty five degrees from the wall on which it pivots. Light, labeled small lambda, is incident from the left side of the wall. Some of the light passes through the open doorway. The light that passes through the door has sharp edges, corresponding to straight edge shadows above and below. The open door also creates a straight edge shadow between it and the wall. Part b of the figure shows a similar diagram. A line parallel to the wall approaches the wall from the left and is labeled plane wave front of sound. There are five dots evenly spaced across the open doorway, labeled one through five. Semicircles appear to the right of these dots entering the room to the right of the wall. Bracketing all these semicircles is a line that has the form of closing square bracket with rounded corners. This line is labeled sound. There are five rays shown pointing from the bracketing line into the room to the right of the wall. Three of these rays point horizontally to the right, one ray points upward and to the right, and the last ray points downward and to the right. This last ray points to the ear of a person who we see from above and who is labeled listener hears sound around the corner.
(a) Light passing through a doorway makes a sharp outline on the floor. Since light’s wavelength is very small compared with the size of the door, it acts like a ray. (b) Sound waves bend into all parts of the room, a wave effect, because their wavelength is similar to the size of the door.

If we pass light through smaller openings such as slits, we can use Huygens’s principle to see that light bends as sound does ( [link] ). The bending of a wave around the edges of an opening or an obstacle is called diffraction. Diffraction is a wave characteristic and occurs for all types of waves. If diffraction is observed for some phenomenon, it is evidence that the phenomenon is a wave. Thus, the horizontal diffraction of the laser beam after it passes through the slits in [link] is evidence that light is a wave. You will learn about diffraction in much more detail in the chapter on Diffraction .

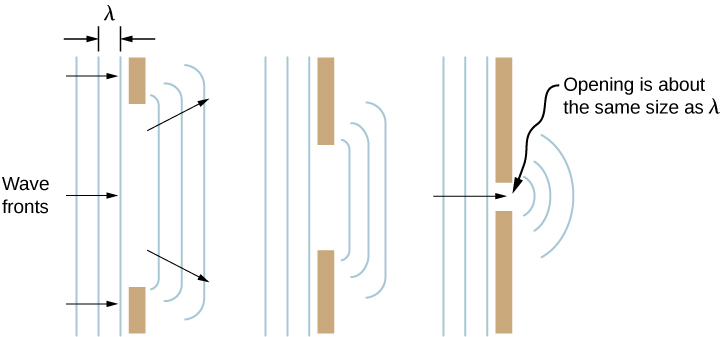
The figure shows three diagrams illustrating waves spreading out when passing through various-size openings. Each illustration is a top view, and the incident plane wave fronts are represented by vertical lines. The wavelength, lambda, is the distance between adjacent lines and is the same in all three diagrams. The first diagram shows wave fronts passing through an opening that is wide compared to the wavelength. The wave fronts that emerge on the other side of the opening have minor bending at the edges. The second diagram shows wave fronts passing through a smaller opening. The waves experience more bending but still have a straight part. The third diagram shows wave fronts passing through an opening that has is about the same size as the wavelength. These waves show significant bending and, in fact, look circular rather than straight.
Huygens’s principle applied to a plane wave front striking an opening. The edges of the wave front bend after passing through the opening, a process called diffraction. The amount of bending is more extreme for a small opening, consistent with the fact that wave characteristics are most noticeable for interactions with objects about the same size as the wavelength.

Summary

  • According to Huygens’s principle, every point on a wave front is a source of wavelets that spread out in the forward direction at the same speed as the wave itself. The new wave front is tangent to all of the wavelets.
  • A mirror reflects an incoming wave at an angle equal to the incident angle, verifying the law of reflection.
  • The law of refraction can be explained by applying Huygens’s principle to a wave front passing from one medium to another.
  • The bending of a wave around the edges of an opening or an obstacle is called diffraction.

Conceptual questions

How do wave effects depend on the size of the object with which the wave interacts? For example, why does sound bend around the corner of a building while light does not?

Got questions? Get instant answers now!

Does Huygens’s principle apply to all types of waves?

yes

Got questions? Get instant answers now!

If diffraction is observed for some phenomenon, it is evidence that the phenomenon is a wave. Does the reverse hold true? That is, if diffraction is not observed, does that mean the phenomenon is not a wave?

Got questions? Get instant answers now!
<< Chapter < Page Page > Chapter >>
Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, University physics volume 3. OpenStax CNX. Nov 04, 2016 Download for free at http://cnx.org/content/col12067/1.4
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'University physics volume 3' conversation and receive update notifications?

Ask