| << Chapter < Page | Chapter >> Page > |
Whenever we look into a mirror, or squint at sunlight glinting from a lake, we are seeing a reflection. When you look at a piece of white paper, you are seeing light scattered from it. Large telescopes use reflection to form an image of stars and other astronomical objects.
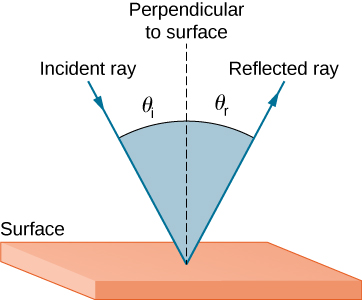
The law of reflection states that the angle of reflection equals the angle of incidence, or
The law of reflection is illustrated in [link] , which also shows how the angle of incidence and angle of reflection are measured relative to the perpendicular to the surface at the point where the light ray strikes.
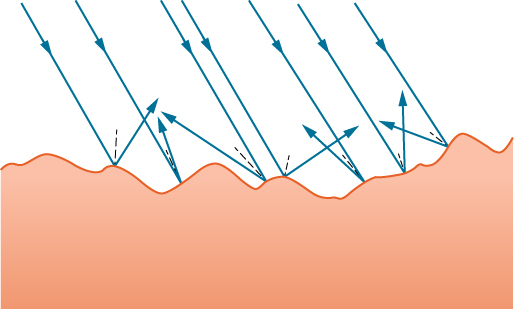
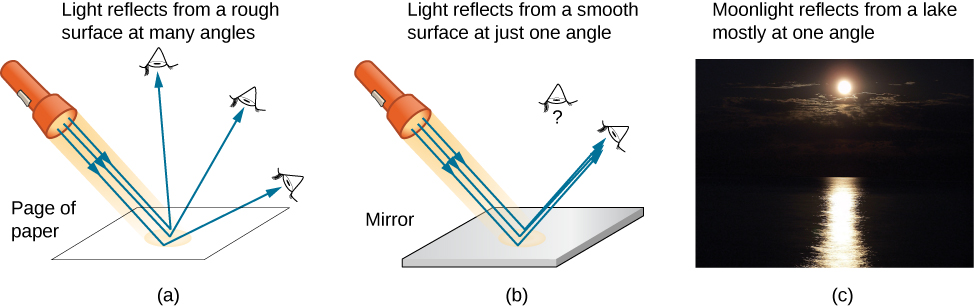
We expect to see reflections from smooth surfaces, but [link] illustrates how a rough surface reflects light. Since the light strikes different parts of the surface at different angles, it is reflected in many different directions, or diffused. Diffused light is what allows us to see a sheet of paper from any angle, as shown in [link] (a). People, clothing, leaves, and walls all have rough surfaces and can be seen from all sides. A mirror, on the other hand, has a smooth surface (compared with the wavelength of light) and reflects light at specific angles, as illustrated in [link] (b). When the Moon reflects from a lake, as shown in [link] (c), a combination of these effects takes place.
When you see yourself in a mirror, it appears that the image is actually behind the mirror ( [link] ). We see the light coming from a direction determined by the law of reflection. The angles are such that the image is exactly the same distance behind the mirror as you stand in front of the mirror. If the mirror is on the wall of a room, the images in it are all behind the mirror, which can make the room seem bigger. Although these mirror images make objects appear to be where they cannot be (like behind a solid wall), the images are not figments of your imagination. Mirror images can be photographed and videotaped by instruments and look just as they do with our eyes (which are optical instruments themselves). The precise manner in which images are formed by mirrors and lenses is discussed in an upcoming chapter on Geometric Optics and Image Formation .

Notification Switch
Would you like to follow the 'University physics volume 3' conversation and receive update notifications?