| << Chapter < Page | Chapter >> Page > |
When a wire is connected between the two ends of a solenoid, the resulting circuit can oscillate like an RLC circuit. Describe what causes the capacitance in this circuit.
Describe what effect the resistance of the connecting wires has on an oscillating LC circuit.
This creates an RLC circuit that dissipates energy, causing oscillations to decrease in amplitude slowly or quickly depending on the value of resistance.
Suppose you wanted to design an LC circuit with a frequency of 0.01 Hz. What problems might you encounter?
A radio receiver uses an RLC circuit to pick out particular frequencies to listen to in your house or car without hearing other unwanted frequencies. How would someone design such a circuit?
You would have to pick out a resistance that is small enough so that only one station at a time is picked up, but big enough so that the tuner doesn’t have to be set at exactly the correct frequency. The inductance or capacitance would have to be varied to tune into the station however practically speaking, variable capacitors are a lot easier to build in a circuit.
In an oscillating RLC circuit, What is the angular frequency of the oscillations?
In an oscillating RLC circuit with how much time elapses before the amplitude of the oscillations drops to half its initial value?
6.9 ms
What resistance R must be connected in series with a 200-mH inductor of the resulting RLC oscillating circuit is to decay to of its initial value of charge in 50 cycles? To of its initial value in 50 cycles?
Show that the self-inductance per unit length of an infinite, straight, thin wire is infinite.
proof
Two long, parallel wires carry equal currents in opposite directions. The radius of each wire is a , and the distance between the centers of the wires is d . Show that if the magnetic flux within the wires themselves can be ignored, the self-inductance of a length l of such a pair of wires is
( Hint : Calculate the magnetic flux through a rectangle of length l between the wires and then use .)
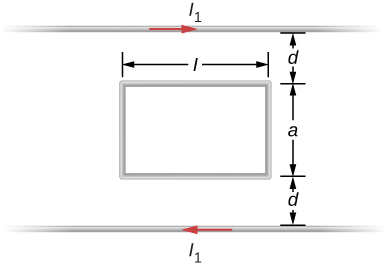
A small, rectangular single loop of wire with dimensions l , and a is placed, as shown below, in the plane of a much larger, rectangular single loop of wire. The two short sides of the larger loop are so far from the smaller loop that their magnetic fields over the smaller fields over the smaller loop can be ignored. What is the mutual inductance of the two loops?
Suppose that a cylindrical solenoid is wrapped around a core of iron whose magnetic susceptibility is x . Using [link] , show that the self-inductance of the solenoid is given by
where l is its length, A its cross-sectional area, and N its total number of turns.
The solenoid of the preceding problem is wrapped around an iron core whose magnetic susceptibility is . (a) If a current of 2.0 A flows through the solenoid, what is the magnetic field in the iron core? (b) What is the effective surface current formed by the aligned atomic current loops in the iron core? (c) What is the self-inductance of the filled solenoid?
a. 100 T; b. 2 A; c. 0.50 H

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?