7.5 Equipotential surfaces and conductors  (Page 6/9)

Can a positively charged conductor be at a negative potential? Explain.

Can equipotential surfaces intersect?

Two very large metal plates are placed 2.0 cm apart, with a potential difference of 12 V between them. Consider one plate to be at 12 V, and the other at 0 V. (a) Sketch the equipotential surfaces for 0, 4, 8, and 12 V. (b) Next sketch in some electric field lines, and confirm that they are perpendicular to the equipotential lines.

A very large sheet of insulating material has had an excess of electrons placed on it to a surface charge density of $\mathrm{–3.00}{\text{nC/m}}^2$ . (a) As the distance from the sheet increases, does the potential increase or decrease? Can you explain why without any calculations? Does the location of your reference point matter? (b) What is the shape of the equipotential surfaces? (c) What is the spacing between surfaces that differ by 1.00 V?

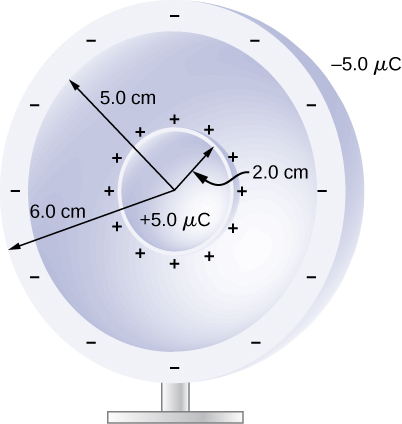
A metallic sphere of radius 2.0 cm is charged with $\text{+}5.0\text{-}\mu \text{C}$ charge, which spreads on the surface of the sphere uniformly. The metallic sphere stands on an insulated stand and is surrounded by a larger metallic spherical shell, of inner radius 5.0 cm and outer radius 6.0 cm. Now, a charge of $\mathrm{-5.0}\text{-}\mu \text{C}$ is placed on the inside of the spherical shell, which spreads out uniformly on the inside surface of the shell. If potential is zero at infinity, what is the potential of (a) the spherical shell, (b) the sphere, (c) the space between the two, (d) inside the sphere, and (e) outside the shell?

Two large charged plates of charge density $\text{±}30\mu {\text{C/m}}^2$ face each other at a separation of 5.0 mm. (a) Find the electric potential everywhere. (b) An electron is released from rest at the negative plate; with what speed will it strike the positive plate?

A long cylinder of aluminum of radius R meters is charged so that it has a uniform charge per unit length on its surface of $\lambda$ .

(a) Find the electric field inside and outside the cylinder. (b) Find the electric potential inside and outside the cylinder. (c) Plot electric field and electric potential as a function of distance from the center of the rod.

Two parallel plates 10 cm on a side are given equal and opposite charges of magnitude $5.0\times {10}^{\mathrm{-9}}\text{C}\text{.}$ The plates are 1.5 mm apart. What is the potential difference between the plates?

The surface charge density on a long straight metallic pipe is $\sigma$ . What is the electric potential outside and inside the pipe? Assume the pipe has a diameter of 2 a .

Concentric conducting spherical shells carry charges Q and – Q , respectively. The inner shell has negligible thickness. What is the potential difference between the shells?

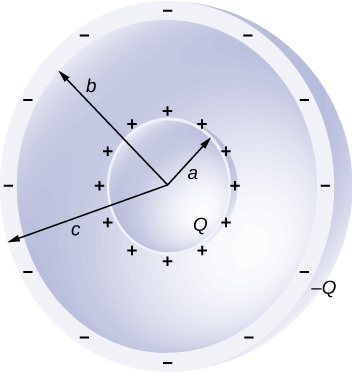
Shown below are two concentric spherical shells of negligible thicknesses and radii $R_1$ and $R_2.$ The inner and outer shell carry net charges $q_1$ and $q_2,$ respectively, where both $q_1$ and $q_2$ are positive. What is the electric potential in the regions (a) $r<R_1,$ (b) $R_1<r<R_2,$ and (c) $r>R_2?$

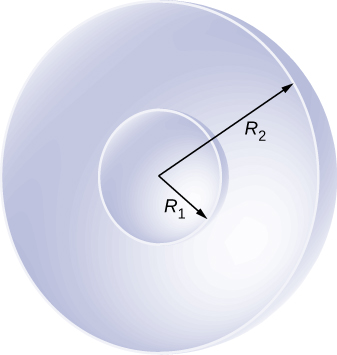
A solid cylindrical conductor of radius a is surrounded by a concentric cylindrical shell of inner radius b . The solid cylinder and the shell carry charges Q and – Q , respectively. Assuming that the length L of both conductors is much greater than a or b , what is the potential difference between the two conductors?