8.1 Capacitors and capacitance  (Page 2/9)

The SI unit of capacitance is the farad (F), named after Michael Faraday (1791–1867). Since capacitance is the charge per unit voltage, one farad is one coulomb per one volt, or

By definition, a 1.0-F capacitor is able to store 1.0 C of charge (a very large amount of charge) when the potential difference between its plates is only 1.0 V. One farad is therefore a very large capacitance. Typical capacitance values range from picofarads $(1\text{pF}={10}^{\text{−}12}\text{F})$ to millifarads $(1\text{mF}={10}^{\text{−}3}\text{F})$ , which also includes microfarads ( $1\mu \text{F}={10}^{\mathrm{-6}}\text{F}$ ). Capacitors can be produced in various shapes and sizes ( [link] ).

Calculation of capacitance

We can calculate the capacitance of a pair of conductors with the standard approach that follows.

To show how this procedure works, we now calculate the capacitances of parallel-plate, spherical, and cylindrical capacitors. In all cases, we assume vacuum capacitors (empty capacitors) with no dielectric substance in the space between conductors.

Parallel-plate capacitor

The parallel-plate capacitor ( [link] ) has two identical conducting plates, each having a surface area A , separated by a distance d . When a voltage V is applied to the capacitor, it stores a charge Q , as shown. We can see how its capacitance may depend on A and d by considering characteristics of the Coulomb force. We know that force between the charges increases with charge values and decreases with the distance between them. We should expect that the bigger the plates are, the more charge they can store. Thus, C should be greater for a larger value of A . Similarly, the closer the plates are together, the greater the attraction of the opposite charges on them. Therefore, C should be greater for a smaller d .

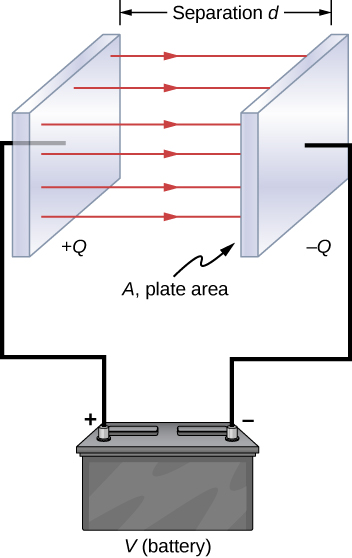
We define the surface charge density $\sigma$ on the plates as

We know from previous chapters that when d is small, the electrical field between the plates is fairly uniform (ignoring edge effects) and that its magnitude is given by

where the constant ${\epsilon }_0$ is the permittivity of free space, ${\epsilon }_0=8.85\times {10}^{\mathrm{-12}}\text{F/m}\text{.}$ The SI unit of F/m is equivalent to ${\text{C}}^2\text{/}\text{N}·{\text{m}}^2.$ Since the electrical field $\overrightarrow{E}$ between the plates is uniform, the potential difference between the plates is

Therefore [link] gives the capacitance of a parallel-plate capacitor as

Notice from this equation that capacitance is a function only of the geometry and what material fills the space between the plates (in this case, vacuum) of this capacitor. In fact, this is true not only for a parallel-plate capacitor, but for all capacitors: The capacitance is independent of Q or V . If the charge changes, the potential changes correspondingly so that Q / V remains constant.