| << Chapter < Page | Chapter >> Page > |
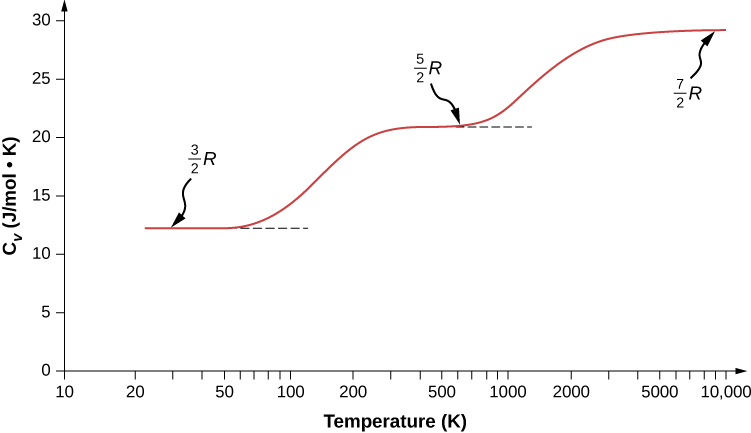
Polyatomic molecules typically have one additional rotational degree of freedom at room temperature, since they have comparable moments of inertia around any axis. Thus, at room temperature, they have and at high temperature, We usually assume that gases have the theoretical room-temperature values of d .
As shown in [link] , the results agree well with experiments for many monatomic and diatomic gases, but the agreement for triatomic gases is only fair. The differences arise from interactions that we have ignored between and within molecules.
| Gas | at and 1 atm |
|---|---|
| Ar | 1.50 |
| He | 1.50 |
| Ne | 1.50 |
| CO | 2.50 |
| 2.47 | |
| 2.50 | |
| 2.53 | |
| 2.8 | |
| 3.48 | |
| 3.13 | |
| 3.66 |
What about internal energy for diatomic and polyatomic gases? For such gases, is a function of temperature ( [link] ), so we do not have the kind of simple result we have for monatomic ideal gases.
The idea of equipartition leads to an estimate of the molar heat capacity of solid elements at ordinary temperatures. We can model the atoms of a solid as attached to neighboring atoms by springs ( [link] ).
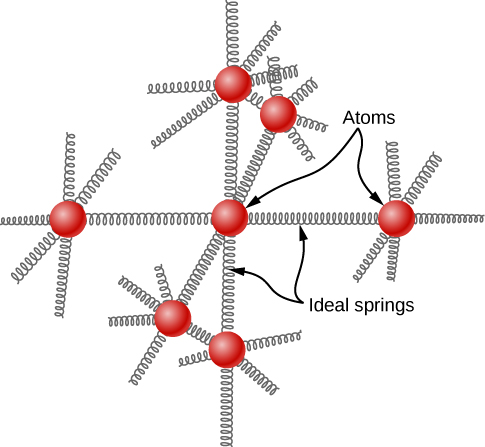
Analogously to the discussion of vibration in the previous module, each atom has six degrees of freedom: one kinetic and one potential for each of the x -, y -, and z -directions. Accordingly, the molar specific heat of a metal should be 3 R . This result, known as the Law of Dulong and Petit , works fairly well experimentally at room temperature. (For every element, it fails at low temperatures for quantum-mechanical reasons. Since quantum effects are particularly important for low-mass particles, the Law of Dulong and Petit already fails at room temperature for some light elements, such as beryllium and carbon. It also fails for some heavier elements for various reasons beyond what we can cover.)
The strategy for solving these problems is the same as the one in Phase Changes for the effects of heat transfer. The only new feature is that you should determine whether the case just presented—ideal gases at constant volume—applies to the problem. (For solid elements, looking up the specific heat capacity is generally better than estimating it from the Law of Dulong and Petit.) In the case of an ideal gas, determine the number d of degrees of freedom from the number of atoms in the gas molecule and use it to calculate (or use to solve for d ).

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?