| << Chapter < Page | Chapter >> Page > |
Note that the reaction does not take place unless there is a complete circuit to allow two electrons to be supplied to the cathode. Under many circumstances, these electrons come from the anode, flow through a resistance, and return to the cathode. Note also that since the chemical reactions involve substances with resistance, it is not possible to create the emf without an internal resistance.
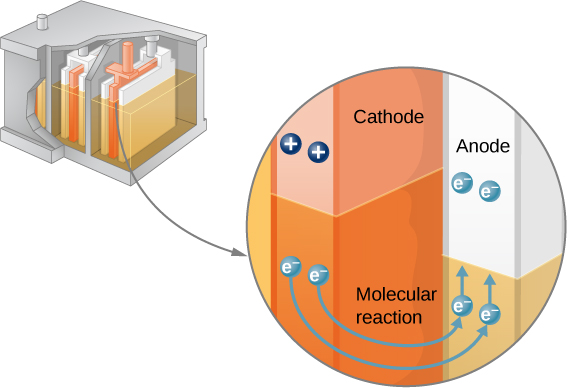
The amount of resistance to the flow of current within the voltage source is called the internal resistance . The internal resistance r of a battery can behave in complex ways. It generally increases as a battery is depleted, due to the oxidation of the plates or the reduction of the acidity of the electrolyte. However, internal resistance may also depend on the magnitude and direction of the current through a voltage source, its temperature, and even its history. The internal resistance of rechargeable nickel-cadmium cells, for example, depends on how many times and how deeply they have been depleted. A simple model for a battery consists of an idealized emf source and an internal resistance r ( [link] ).

Suppose an external resistor, known as the load resistance R , is connected to a voltage source such as a battery, as in [link] . The figure shows a model of a battery with an emf , an internal resistance r , and a load resistor R connected across its terminals. Using conventional current flow, positive charges leave the positive terminal of the battery, travel through the resistor, and return to the negative terminal of the battery. The terminal voltage of the battery depends on the emf, the internal resistance, and the current, and is equal to
For a given emf and internal resistance, the terminal voltage decreases as the current increases due to the potential drop Ir of the internal resistance.
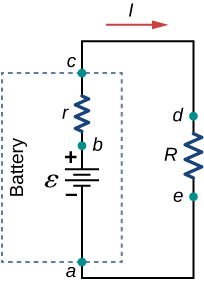
A graph of the potential difference across each element the circuit is shown in [link] . A current I runs through the circuit, and the potential drop across the internal resistor is equal to Ir . The terminal voltage is equal to , which is equal to the potential drop across the load resistor . As with potential energy, it is the change in voltage that is important. When the term “voltage” is used, we assume that it is actually the change in the potential, or . However, is often omitted for convenience.

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?