12.1 The biot-savart law (Page 2/4)

University physics volume 2 Page 2 / 4

Calculating magnetic fields of short current segments

A short wire of length 1.0 cm carries a current of 2.0 A in the vertical direction ( [link] ). The rest of the wire is shielded so it does not add to the magnetic field produced by the wire. Calculate the magnetic field at point P , which is 1 meter from the wire in the x -direction.

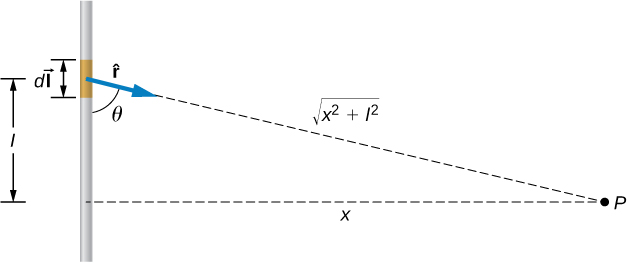
This figure shows a wire I with a short unshielded piece dI that carries current. Point P is located at the distance x from the wire. A vector to the point P from dI forms an angle theta with the wire. The length of the vector is the square root of the sums of squares of x and I. — A small line segment carries a current I in the vertical direction. What is the magnetic field at a distance x from the segment?

Strategy

We can determine the magnetic field at point P using the Biot-Savart law. Since the current segment is much smaller than the distance x , we can drop the integral from the expression. The integration is converted back into a summation, but only for small dl , which we now write as

Δ l .

Another way to think about it is that each of the radius values is nearly the same, no matter where the current element is on the line segment, if

Δ l

is small compared to x . The angle

θ

is calculated using a tangent function. Using the numbers given, we can calculate the magnetic field at P .

Solution

The angle between

Δ \vec{l}

and

\hat{r}

is calculated from trigonometry, knowing the distances l and x from the problem:

θ = {tan}^{−1} (\frac{1 m}{0.01 m}) = 89.4 ° .

The magnetic field at point P is calculated by the Biot-Savart law:

B = \frac{μ_{0}}{4 π} \frac{I Δ l sin θ}{r^{2}} = (1 \times 10^{−7} T \cdot m/A) (\frac{2 A (0.01 m) sin (89.4 °)}{{(1 m)}^{2}}) = 2.0 \times 10^{−9} T .

From the right-hand rule and the Biot-Savart law, the field is directed into the page.

Significance

This approximation is only good if the length of the line segment is very small compared to the distance from the current element to the point. If not, the integral form of the Biot-Savart law must be used over the entire line segment to calculate the magnetic field.

Got questions? Get instant answers now!

Check Your Understanding Using [link] , at what distance would P have to be to measure a magnetic field half of the given answer?

1.41 meters

Got questions? Get instant answers now!

Calculating magnetic field of a circular arc of wire

A wire carries a current I in a circular arc with radius R swept through an arbitrary angle

θ

( [link] ). Calculate the magnetic field at the center of this arc at point P .

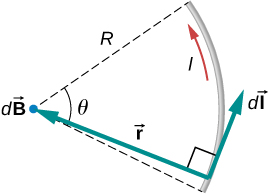
This figure shows a piece of wire in the shape of a circular arc with radius R swept through an arbitrary angle theta. Wire carries a current dI. Point P is located at the center. A vector r to the point P is perpendicular to the vector dI. — A wire segment carrying a current I . The path $d \vec{l}$ and radial direction $\hat{r}$ are indicated.

Strategy

We can determine the magnetic field at point P using the Biot-Savart law. The radial and path length directions are always at a right angle, so the cross product turns into multiplication. We also know that the distance along the path dl is related to the radius times the angle

θ

(in radians). Then we can pull all constants out of the integration and solve for the magnetic field.

Solution

The Biot-Savart law starts with the following equation:

\vec{B} = \frac{μ_{0}}{4 π} \int_{wire} \frac{I d \vec{l} \times \hat{r}}{r^{2}} .

As we integrate along the arc, all the contributions to the magnetic field are in the same direction (out of the page), so we can work with the magnitude of the field. The cross product turns into multiplication because the path dl and the radial direction are perpendicular. We can also substitute the arc length formula, $d l = r d θ$ :

B = \frac{μ_{0}}{4 π} \int_{wire} \frac{I r d θ}{r^{2}} .

The current and radius can be pulled out of the integral because they are the same regardless of where we are on the path. This leaves only the integral over the angle,

B = \frac{μ_{0} I}{4 π r} \int_{wire} d θ .

The angle varies on the wire from 0 to $θ$ ; hence, the result is

B = \frac{μ_{0} I θ}{4 π r} .

Significance

The direction of the magnetic field at point P is determined by the right-hand rule, as shown in the previous chapter. If there are other wires in the diagram along with the arc, and you are asked to find the net magnetic field, find each contribution from a wire or arc and add the results by superposition of vectors. Make sure to pay attention to the direction of each contribution. Also note that in a symmetric situation, like a straight or circular wire, contributions from opposite sides of point P cancel each other.

Got questions? Get instant answers now!

Check Your Understanding The wire loop forms a full circle of radius R and current I . What is the magnitude of the magnetic field at the center?

$\frac{μ_{0} I}{2 R}$

Got questions? Get instant answers now!

Summary

The magnetic field created by a current-carrying wire is found by the Biot-Savart law.
The current element $I d \vec{l}$ produces a magnetic field a distance r away.

Conceptual questions

For calculating magnetic fields, what are the advantages and disadvantages of the Biot-Savart law?

Biot-Savart law’s advantage is that it works with any magnetic field produced by a current loop. The disadvantage is that it can take a long time.

Got questions? Get instant answers now!

Describe the magnetic field due to the current in two wires connected to the two terminals of a source of emf and twisted tightly around each other.

Got questions? Get instant answers now!

How can you decide if a wire is infinite?

If you were to go to the start of a line segment and calculate the angle $θ$ to be approximately $0 °$ , the wire can be considered infinite. This judgment is based also on the precision you need in the result.

Got questions? Get instant answers now!

Identical currents are carried in two circular loops; however, one loop has twice the diameter as the other loop. Compare the magnetic fields created by the loops at the center of each loop.

Got questions? Get instant answers now!

Problems

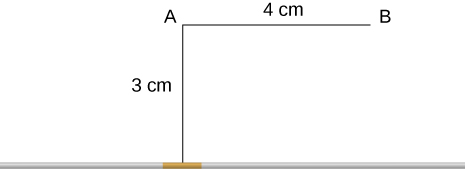
A 10-A current flows through the wire shown. What is the magnitude of the magnetic field due to a 0.5-mm segment of wire as measured at (a) point A and (b) point B?

This figure shows a piece of wire. Point A is located 3 centimeters above the 0.5 mm segment of wire. Point B is located 4 centimeters to the right of point A.

Got questions? Get instant answers now!

Ten amps flow through a square loop where each side is 20 cm in length. At each corner of the loop is a 0.01-cm segment that connects the longer wires as shown. Calculate the magnitude of the magnetic field at the center of the loop.

A square loop is shown with rounded corners. There are no markings.

$1 \times 10^{−8} T$

Got questions? Get instant answers now!

What is the magnetic field at P due to the current I in the wire shown?

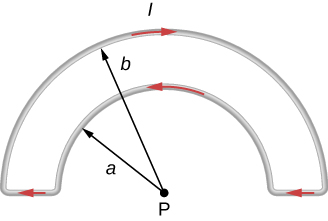
This figure shows a current loop consisting of two concentric circular arcs and two parallel radial lines. Outer arc is located at the distance b from the center; inner arc is located at the distance a from the center.

Got questions? Get instant answers now!

The accompanying figure shows a current loop consisting of two concentric circular arcs and two perpendicular radial lines. Determine the magnetic field at point P.

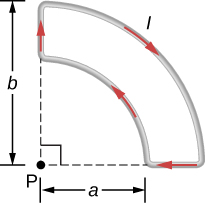
This figure shows a current loop consisting of two concentric circular arcs and two perpendicular radial lines. Outer arc is located at the distance b from the center; inner arc is located at the distance a from the center.

$B = \frac{μ_{o} I}{8} (\frac{1}{a} - \frac{1}{b})$ out of the page

Got questions? Get instant answers now!

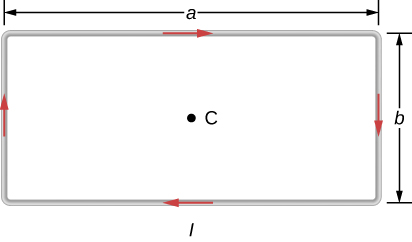
Find the magnetic field at the center C of the rectangular loop of wire shown in the accompanying figure.

This figure shows a rectangular current loop. The length of the short side is b; the length of the long side is a. Point C is a center of the loop.

Got questions? Get instant answers now!

Two long wires, one of which has a semicircular bend of radius R , are positioned as shown in the accompanying figure. If both wires carry a current I , how far apart must their parallel sections be so that the net magnetic field at P is zero? Does the current in the straight wire flow up or down?

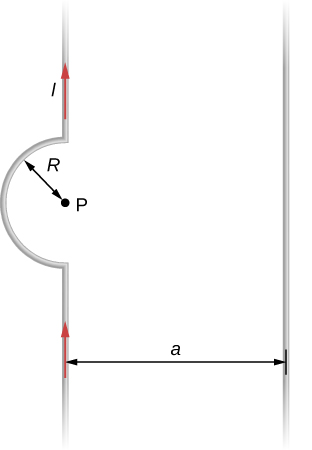
This figure shows two parallel long wires located at a distance a from each other. One of the wires has a semicircular bend of radius R.

$a = \frac{2 R}{π}$ ; the current in the wire to the right must flow up the page.

Got questions? Get instant answers now!

<< Chapter < Page Page > Chapter >>

Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, University physics volume 2. OpenStax CNX. Oct 06, 2016 Download for free at http://cnx.org/content/col12074/1.3

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'University physics volume 2' conversation and receive update notifications?

Ask

	3 Psychology MCQ 2009 2 Exam By John Gabrieli Start Exam
	3 Physiotherapy Flashcards Set 3 By Rhodes Start Flashcards
	Anthropology Language Culture By Richley Crapo Start Assignment
	Principles of economics By OpenStax Read Online Course
	24 PLANT QUIZ 1 By Brooke Delaney Start Exam
	3 Lec:3 Cohort Studies By Janet Forrester Start Quiz
	Psychology By OpenStax Read Online Course
	23 Biology 23 Protists MCQ By OpenStax Start Quiz
	9 AP 09 Joints Essay Quiz By OpenStax Start Flashcards
	NCE Ch 08 Appraisal By Anh Dao Start Quiz