4.4 Statements of the second law of thermodynamics  (Page 2/5)

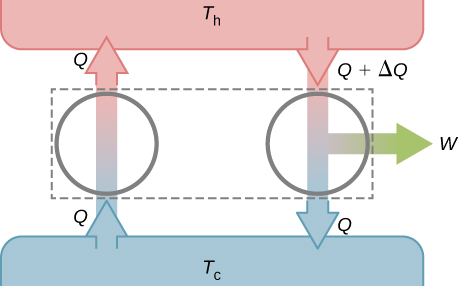
Suppose these two devices are combined as shown in [link] . The net heat removed from the hot reservoir is $\text{Δ}Q$ , no net heat transfer occurs to or from the cold reservoir, and work W is done on some external body. Since $W=\text{Δ}Q$ , the combination of a perfect refrigerator and a real heat engine is itself a perfect heat engine, thereby contradicting the Kelvin statement. Thus, if the Clausius statement is false, the Kelvin statement must also be false.

Using the second law of thermodynamics, we now prove two important properties of heat engines operating between two heat reservoirs. The first property is that any reversible engine operating between two reservoirs has a greater efficiency than any irreversible engine operating between the same two reservoirs .

The second property to be demonstrated is that all reversible engines operating between the same two reservoirs have the same efficiency . To show this, we start with the two engines D and E of [link] (a), which are operating between two common heat reservoirs at temperatures $T_{\text{h}}\text{and}{T}_{\text{c}}.$ First, we assume that D is a reversible engine and that E is a hypothetical irreversible engine that has a higher efficiency than D. If both engines perform the same amount of work $W$ per cycle, it follows from [link] that $Q_{\text{h}}>Q_{\text{h}}^{\prime }$ . It then follows from the first law that $Q_{\text{c}}>Q_{\text{c}}^{\prime }.$

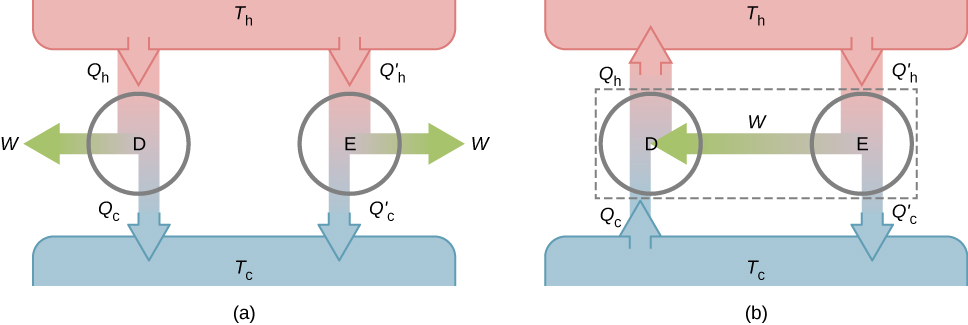
Suppose the cycle of D is reversed so that it operates as a refrigerator, and the two engines are coupled such that the work output of E is used to drive D, as shown in [link] (b). Since $Q_{\text{h}}>Q_{\text{h}}^{\prime }$ and $Q_{\text{c}}>Q_{\text{c}}^{\prime },$ the net result of each cycle is equivalent to a spontaneous transfer of heat from the cold reservoir to the hot reservoir, a process the second law does not allow. The original assumption must therefore be wrong, and it is impossible to construct an irreversible engine such that E is more efficient than the reversible engine D.

Now it is quite easy to demonstrate that the efficiencies of all reversible engines operating between the same reservoirs are equal. Suppose that D and E are both reversible engines. If they are coupled as shown in [link] (b), the efficiency of E cannot be greater than the efficiency of D, or the second law would be violated. If both engines are then reversed, the same reasoning implies that the efficiency of D cannot be greater than the efficiency of E. Combining these results leads to the conclusion that all reversible engines working between the same two reservoirs have the same efficiency.

Summary

• The Kelvin statement of the second law of thermodynamics: It is impossible to convert the heat from a single source into work without any other effect.
• The Kelvin statement and Clausius statement of the second law of thermodynamics are equivalent.

Conceptual questions