14.1 Mutual inductance (Page 2/5)

University physics volume 2 Page 2 / 5

A large mutual inductance M may or may not be desirable. We want a transformer to have a large mutual inductance. But an appliance, such as an electric clothes dryer, can induce a dangerous emf on its metal case if the mutual inductance between its coils and the case is large. One way to reduce mutual inductance is to counter-wind coils to cancel the magnetic field produced ( [link] ).

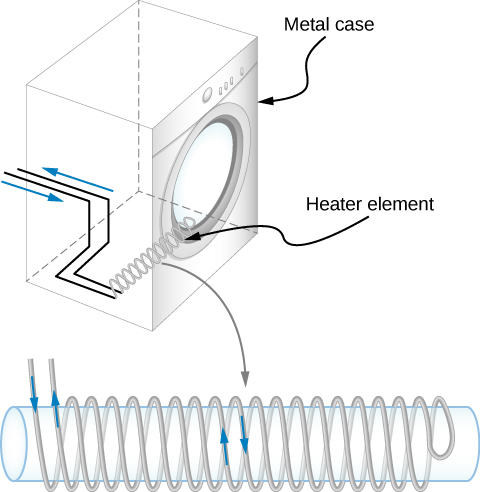
Figure a shows a heating coil within a metal case of a clothes dryer. Figure b shows the same coil, enlarged. The coil is wound on a cylinder in such a way that one wire is wound all the way to the other side, twisted around and wound all the way back. Thus, two adjacent windings have current flowing in opposite directions. — The heating coils of an electric clothes dryer can be counter-wound so that their magnetic fields cancel one another, greatly reducing the mutual inductance with the case of the dryer.

Digital signal processing is another example in which mutual inductance is reduced by counter-winding coils. The rapid on/off emf representing 1s and 0s in a digital circuit creates a complex time-dependent magnetic field. An emf can be generated in neighboring conductors. If that conductor is also carrying a digital signal, the induced emf may be large enough to switch 1s and 0s, with consequences ranging from inconvenient to disastrous.

Mutual inductance

[link] shows a coil of

N_{2}

turns and radius

R_{2}

surrounding a long solenoid of length

l_{1},

radius

R_{1},

and

N_{1}

turns. (a) What is the mutual inductance of the two coils? (b) If

N_{1} = 500 turns

N_{2} = 10 turns

R_{1} = 3.10 cm

l_{1} = 75.0 cm

, and the current in the solenoid is changing at a rate of 200 A/s, what is the emf induced in the surrounding coil?

Figure shows a solenoid, in the form of a long coil with a small diameter, that is concentrically arranged with another, bigger coil. The radius of the solenoid is R1 and that of the coil is R2. The length of the solenoid is l1. — A solenoid surrounded by a coil.

Strategy

There is no magnetic field outside the solenoid, and the field inside has magnitude

B_{1} = μ_{0} (N_{1} / l_{1}) I_{1}

and is directed parallel to the solenoid’s axis. We can use this magnetic field to find the magnetic flux through the surrounding coil and then use this flux to calculate the mutual inductance for part (a), using [link] . We solve part (b) by calculating the mutual inductance from the given quantities and using [link] to calculate the induced emf.

Solution

The magnetic flux $Φ_{21}$ through the surrounding coil is

$Φ_{21} = B_{1} π R_{1}^{2} = \frac{μ_{0} N_{1} I_{1}}{l_{1}} π R_{1}^{2} .$

Now from [link] , the mutual inductance is

$M = \frac{N_{2} Φ_{21}}{I_{1}} = (\frac{N_{2}}{I_{1}}) (\frac{μ_{0} N_{1} I_{1}}{l_{1}}) π R_{1}^{2} = \frac{μ_{0} N_{1} N_{2} π R_{1}^{2}}{l_{1}} .$
Using the previous expression and the given values, the mutual inductance is

$\begin{matrix} M & = \frac{(4 π \times 10^{−7} T \cdot m/A) (500) (10) π {(0.0310 m)}^{2}}{0.750 m} \\ = 2.53 \times 10^{−5} H . \end{matrix}$

Thus, from [link] , the emf induced in the surrounding coil is

$\begin{matrix} ε_{2} & = − M \frac{d I_{1}}{d t} = − (2.53 \times 10^{−5} H) (200 A/s) \\ = −5.06 \times 10^{−3} V . \end{matrix}$

Significance

Notice that M in part (a) is independent of the radius

R_{2}

of the surrounding coil because the solenoid’s magnetic field is confined to its interior. In principle, we can also calculate M by finding the magnetic flux through the solenoid produced by the current in the surrounding coil. This approach is much more difficult because

Φ_{12}

is so complicated. However, since

M_{12} = M_{21},

we do know the result of this calculation.

Got questions? Get instant answers now!

Check Your Understanding A current $I (t) = (5.0 A) sin ((120 π rad/s) t)$ flows through the solenoid of part (b) of [link] . What is the maximum emf induced in the surrounding coil?

$4.77 \times 10^{−2} V$

Got questions? Get instant answers now!

Summary

Inductance is the property of a device that expresses how effectively it induces an emf in another device.
Mutual inductance is the effect of two devices inducing emfs in each other.
A change in current ${d I}_{1} / d t$ in one circuit induces an emf $(ε_{2})$ in the second:

$ε_{2} = - M \frac{d I 1}{d t},$

where M is defined to be the mutual inductance between the two circuits and the minus sign is due to Lenz’s law.
Symmetrically, a change in current ${d I}_{2} / d t$ through the second circuit induces an emf $(ε_{1})$ in the first:

$ε_{1} = - M \frac{d I_{2}}{d t},$

where M is the same mutual inductance as in the reverse process.

Conceptual questions

Show that $N Φ_{m} / I$ and $ε / (d I / d t),$ which are both expressions for self-inductance, have the same units.

$\frac{Wb}{A} = \frac{T \cdot m^{2}}{A} = \frac{V \cdot s}{A} = \frac{V}{A/s}$

Got questions? Get instant answers now!

A 10-H inductor carries a current of 20 A. Describe how a 50-V emf can be induced across it.

Got questions? Get instant answers now!

The ignition circuit of an automobile is powered by a 12-V battery. How are we able to generate large voltages with this power source?

The induced current from the 12-V battery goes through an inductor, generating a large voltage.

Got questions? Get instant answers now!

When the current through a large inductor is interrupted with a switch, an arc appears across the open terminals of the switch. Explain.

Got questions? Get instant answers now!

Problems

When the current in one coil changes at a rate of 5.6 A/s, an emf of $6.3 \times 10^{−3} V$ is induced in a second, nearby coil. What is the mutual inductance of the two coils?

Got questions? Get instant answers now!

An emf of $9.7 \times 10^{−3} V$ is induced in a coil while the current in a nearby coil is decreasing at a rate of 2.7 A/s. What is the mutual inductance of the two coils?

$M = 3.6 \times 10^{−3} H$

Got questions? Get instant answers now!

Two coils close to each other have a mutual inductance of 32 mH. If the current in one coil decays according to $I = I_{0} e^{− α t}$ , where $I_{0} = 5.0 A$ and $α = 2.0 \times 10^{3} s^{−1},$ what is the emf induced in the second coil immediately after the current starts to decay? At $t = 1.0 \times 10^{−3} s ?$

Got questions? Get instant answers now!

A coil of 40 turns is wrapped around a long solenoid of cross-sectional area $7.5 \times 10^{−3} m^{2} .$ The solenoid is 0.50 m long and has 500 turns. (a) What is the mutual inductance of this system? (b) The outer coil is replaced by a coil of 40 turns whose radius is three times that of the solenoid. What is the mutual inductance of this configuration?

a. $3.8 \times 10^{−4} H$ ; b. $3.8 \times 10^{−4} H$

Got questions? Get instant answers now!

A 600-turn solenoid is 0.55 m long and 4.2 cm in diameter. Inside the solenoid, a small $(1.1 cm \times 1.4 cm),$ single-turn rectangular coil is fixed in place with its face perpendicular to the long axis of the solenoid. What is the mutual inductance of this system?

Got questions? Get instant answers now!

A toroidal coil has a mean radius of 16 cm and a cross-sectional area of ${0.25 cm}^{2}$ ; it is wound uniformly with 1000 turns. A second toroidal coil of 750 turns is wound uniformly over the first coil. Ignoring the variation of the magnetic field within a toroid, determine the mutual inductance of the two coils.

$M_{21} = 2.3 \times 10^{−5} H$

Got questions? Get instant answers now!

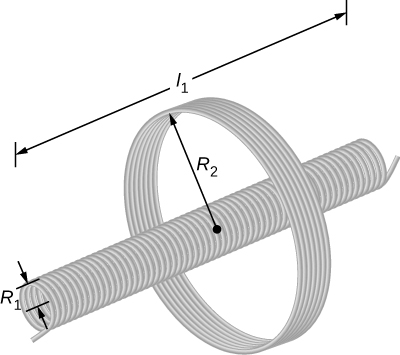
A solenoid of $N_{1}$ turns has length $l_{1}$ and radius $R_{1},$ and a second smaller solenoid of $N_{2}$ turns has length $l_{2}$ and radius $R_{2}$ . The smaller solenoid is placed completely inside the larger solenoid so that their long axes coincide. What is the mutual inductance of the two solenoids?

Got questions? Get instant answers now!

<< Chapter < Page Page > Chapter >>

Practice Key Terms 3

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, University physics volume 2. OpenStax CNX. Oct 06, 2016 Download for free at http://cnx.org/content/col12074/1.3

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'University physics volume 2' conversation and receive update notifications?

Ask

	Young Economist MCQ Test By Robert Murphy Start Test
	3 Psychology MCQ 2009 2 Exam By John Gabrieli Start Exam
	3 Enterprise Java Design Patterns By JavaChamp Team Start Quiz
	English Proficiency Test By Anindyo Mukhopadhyay Start Quiz
	2 Understanding Societies 2 By Jessica Collett Start Exam
©flickr: Eduardo	Nursing Education NU589 Program Outcomes By Karen Gowdey Start Quiz
	25 AP 25 Urinary System Essay By OpenStax Start Flashcards
	Job Search Skills MCQ By Mary Matera Start Quiz
	1 Sociology 01 An Introduction to Sociology MCQ By OpenStax Start Quiz
	Time and Stress Management MCQ By Dionne Mahaffey Start Quiz