1. Home
  2. University physics volume 2
  3. Unit 2. electricity and magnetism
  4. Magnetic forces and fields
  5. Magnetic force on a current

11.4 Magnetic force on a current-carrying conductor  (Page 3/3)

<< Chapter < Page
  University physics volume 2     Page 3 / 3
Chapter >> Page >

Solution

  1. We start with the general formula for the magnetic force on a wire. We are looking for the force per unit length, so we divide by the length to bring it to the left-hand side. We also set sin θ = 1 . The solution therefore is
    F = I l B sin θ F l = ( 5.0 A ) ( 0.30 T ) F l = 1.5 N/m.

    Directionality: Point your fingers in the positive y -direction and curl your fingers in the positive x -direction. Your thumb will point in the − k → direction. Therefore, with directionality, the solution is
    F → l = −1.5 k → N/m.
  2. The current times length and the magnetic field are written in unit vector notation. Then, we take the cross product to find the force:
    F → = I l → × B → = ( 5.0 A ) l j ^ × ( 0.30 T cos ( 30 ° ) i ^ + 0.30 T sin ( 30 ° ) j ^ ) F → / l = −1.30 k ^ N/m.

Significance

This large magnetic field creates a significant force on a small length of wire. As the angle of the magnetic field becomes more closely aligned to the current in the wire, there is less of a force on it, as seen from comparing parts a and b.

Check Your Understanding A straight, flexible length of copper wire is immersed in a magnetic field that is directed into the page. (a) If the wire’s current runs in the + x -direction, which way will the wire bend? (b) Which way will the wire bend if the current runs in the – x -direction?

a. bends upward; b. bends downward

Got questions? Get instant answers now!

Force on a circular wire

A circular current loop of radius R carrying a current I is placed in the xy -plane. A constant uniform magnetic field cuts through the loop parallel to the y -axis ( [link] ). Find the magnetic force on the upper half of the loop, the lower half of the loop, and the total force on the loop.

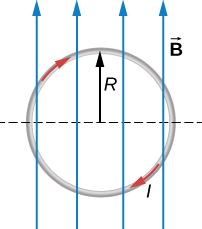
A loop of radius R is in the plane of the page. The loop carries a clockwise current I and is in a uniform magnetic field that points up the page.
A loop of wire carrying a current in a magnetic field.

Strategy

The magnetic force on the upper loop should be written in terms of the differential force acting on each segment of the loop. If we integrate over each differential piece, we solve for the overall force on that section of the loop. The force on the lower loop is found in a similar manner, and the total force is the addition of these two forces.

Solution

A differential force on an arbitrary piece of wire located on the upper ring is:

d F = I B sin θ d l .

where θ is the angle between the magnetic field direction (+ y ) and the segment of wire. A differential segment is located at the same radius, so using an arc-length formula, we have:

d l = R d θ d F = I B R sin θ d θ .

In order to find the force on a segment, we integrate over the upper half of the circle, from 0 to π . This results in:

F = I B R ∫ 0 π sin θ d θ = I B R ( − cos π + cos 0 ) = 2 I B R .

The lower half of the loop is integrated from π to zero, giving us:

F = I B R ∫ π 0 sin θ d θ = I B R ( − cos 0 + cos π ) = −2 I B R .

The net force is the sum of these forces, which is zero.

Significance

The total force on any closed loop in a uniform magnetic field is zero. Even though each piece of the loop has a force acting on it, the net force on the system is zero. (Note that there is a net torque on the loop, which we consider in the next section.)

Got questions? Get instant answers now!

Summary

  • An electrical current produces a magnetic field around the wire.
  • The directionality of the magnetic field produced is determined by the right hand rule-2, where your thumb points in the direction of the current and your fingers wrap around the wire in the direction of the magnetic field.
  • The magnetic force on current-carrying conductors is given by F → = I l → × B → where I is the current and l is the length of a wire in a uniform magnetic field B .

Conceptual questions

Describe the error that results from accidently using your left rather than your right hand when determining the direction of a magnetic force.

Got questions? Get instant answers now!

Considering the magnetic force law, are the velocity and magnetic field always perpendicular? Are the force and velocity always perpendicular? What about the force and magnetic field?

Velocity and magnetic field can be set together in any direction. If there is a force, the velocity is perpendicular to it. The magnetic field is also perpendicular to the force if it exists.

Got questions? Get instant answers now!

Why can a nearby magnet distort a cathode ray tube television picture?

Got questions? Get instant answers now!

A magnetic field exerts a force on the moving electrons in a current carrying wire. What exerts the force on a wire?

A force on a wire is exerted by an external magnetic field created by a wire or another magnet.

Got questions? Get instant answers now!

There are regions where the magnetic field of earth is almost perpendicular to the surface of Earth. What difficulty does this cause in the use of a compass?

Got questions? Get instant answers now!

Problems

What is the direction of the magnetic force on the current in each of the six cases?

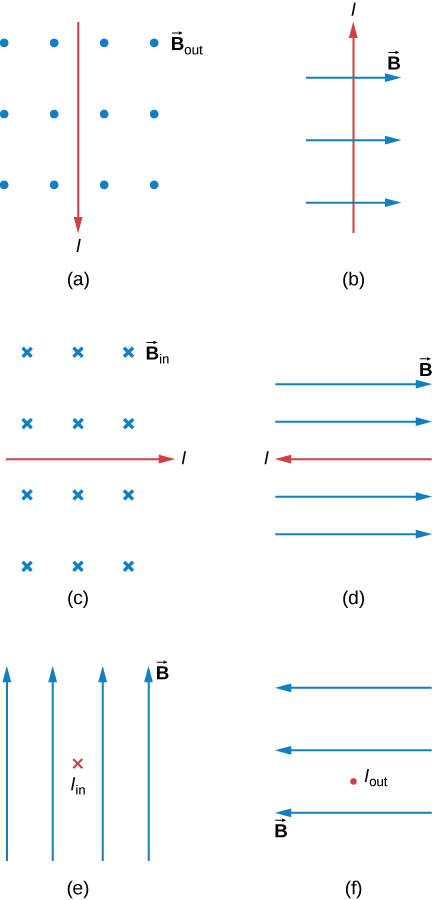
Case a: I is down, B is out of the page. Case b: I is up, B is to the right. Case c: I is to the right, B is into the page. Case d: I is to the left , B is to the right. Case e: I is into the page, B is up. Case f: I is out of the page, B is to the left.

a. left; b. into the page; c. up; d. no force; e. right; f. down

Got questions? Get instant answers now!

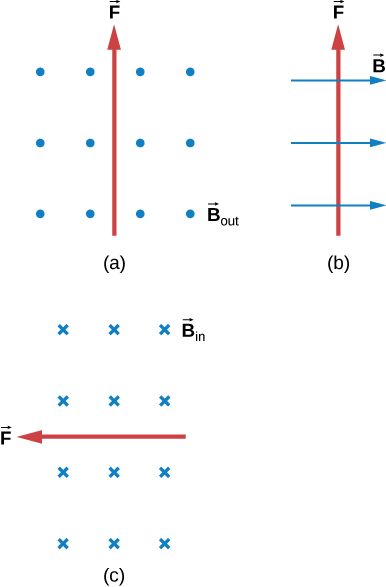
What is the direction of a current that experiences the magnetic force shown in each of the three cases, assuming the current runs perpendicular to B → ?

Case a: B is out of the page, F is up. Case b: B is to the right, F is up. Case c: B is into the page, F is to the left.
Got questions? Get instant answers now!

What is the direction of the magnetic field that produces the magnetic force shown on the currents in each of the three cases, assuming B → is perpendicular to I ?

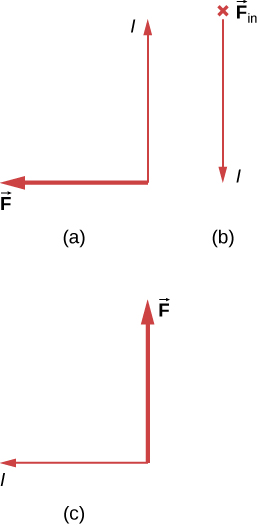
Case a: I is up, F is to the left. Case b: I is down, F is into the page. Case c: I is to the left, F is up.

a. into the page; b. left; c. out of the page

Got questions? Get instant answers now!

(a) What is the force per meter on a lightning bolt at the equator that carries 20,000 A perpendicular to Earth’s 3.0 × 10 −5 T field? (b) What is the direction of the force if the current is straight up and Earth’s field direction is due north, parallel to the ground?

Got questions? Get instant answers now!

(a) A dc power line for a light-rail system carries 1000 A at an angle of 30.0º to Earth’s 5.0 × 10 −5 T field. What is the force on a 100-m section of this line? (b) Discuss practical concerns this presents, if any.

a. 2.50 N; b. This means that the light-rail power lines must be attached in order not to be moved by the force caused by Earth’s magnetic field.

Got questions? Get instant answers now!

A wire carrying a 30.0-A current passes between the poles of a strong magnet that is perpendicular to its field and experiences a 2.16-N force on the 4.00 cm of wire in the field. What is the average field strength?

Got questions? Get instant answers now!
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, University physics volume 2. OpenStax CNX. Oct 06, 2016 Download for free at http://cnx.org/content/col12074/1.3
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'University physics volume 2' conversation and receive update notifications?

Ask