12.7 Magnetism in matter  (Page 5/13)

A charge of $4.0\text{μC}$ is distributed uniformly around a thin ring of insulating material. The ring has a radius of 0.20 m and rotates at $2.0\times {10}^4\text{rev/min}$ around the axis that passes through its center and is perpendicular to the plane of the ring. What is the magnetic field at the center of the ring?

A thin, nonconducting disk of radius R is free to rotate around the axis that passes through its center and is perpendicular to the face of the disk. The disk is charged uniformly with a total charge q . If the disk rotates at a constant angular velocity $\omega ,$ what is the magnetic field at its center?

Consider the disk in the previous problem. Calculate the magnetic field at a point on its central axis that is a distance y above the disk.

Consider the axial magnetic field $B_v={\mu }_{0}I{R}^2\text{/}2(y^2+R^2{)}^{3\text{/}2}$ of the circular current loop shown below. (a) Evaluate ${\displaystyle {\int }_{\text{−}a}^a{B}_{y}dy.}$ Also show that $\underset{a\to \infty }{\text{lim}}{\displaystyle {\int }_{\text{−}a}^a{B}_y}dy={\mu }_{0}I.$ (b) Can you deduce this limit without evaluating the integral? ( Hint: See the accompanying figure.)

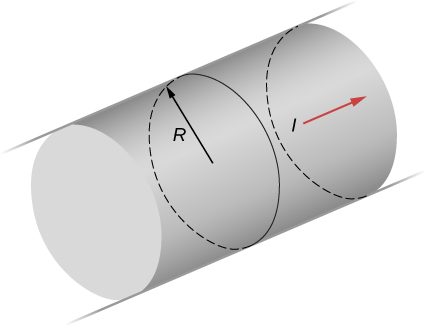
The current density in the long, cylindrical wire shown in the accompanying figure varies with distance r from the center of the wire according to $J=cr,$ where c is a constant. (a) What is the current through the wire? (b) What is the magnetic field produced by this current for $r\le R?$ For $r\ge R?$

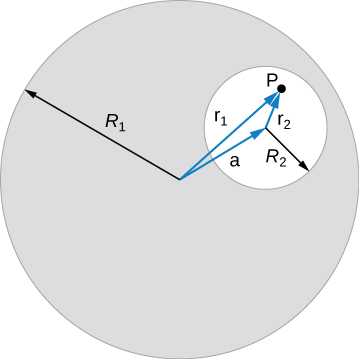
A long, straight, cylindrical conductor contains a cylindrical cavity whose axis is displaced by a from the axis of the conductor, as shown in the accompanying figure. The current density in the conductor is given by $\overrightarrow{J}=J_0\widehat{k},$ where $J_0$ is a constant and $\widehat{k}$ is along the axis of the conductor. Calculate the magnetic field at an arbitrary point P in the cavity by superimposing the field of a solid cylindrical conductor with radius $R_1$ and current density $\overrightarrow{J}$ onto the field of a solid cylindrical conductor with radius $R_2$ and current density $\text{−}\overrightarrow{J}.$ Then use the fact that the appropriate azimuthal unit vectors can be expressed as ${\widehat{\theta }}_1=\widehat{k}\times {\widehat{r}}_1$ and ${\widehat{\theta }}_2=\widehat{k}\times {\widehat{r}}_2$ to show that everywhere inside the cavity the magnetic field is given by the constant $\overrightarrow{B}=\frac{1}{2}{\mu }_0{J}_{0}k\times a,$ where $a=r_1-r_2$ and $r_1=r_1{\widehat{r}}_1$ is the position of P relative to the center of the conductor and $r_2=r_2{\widehat{r}}_2$ is the position of P relative to the center of the cavity.

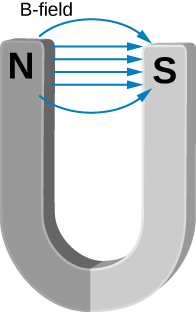
Between the two ends of a horseshoe magnet the field is uniform as shown in the diagram. As you move out to outside edges, the field bends. Show by Ampère’s law that the field must bend and thereby the field weakens due to these bends.

Show that the magnetic field of a thin wire and that of a current loop are zero if you are infinitely far away.

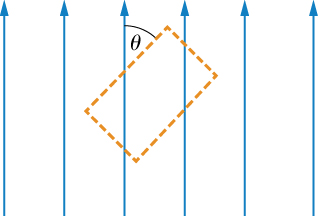
An Ampère loop is chosen as shown by dashed lines for a parallel constant magnetic field as shown by solid arrows. Calculate $\overrightarrow{B}·d\overrightarrow{l}$ for each side of the loop then find the entire ${\displaystyle \oint \overrightarrow{B}}·d\overrightarrow{l}.$ Can you think of an Ampère loop that would make the problem easier? Do those results match these?

A very long, thick cylindrical wire of radius R carries a current density J that varies across its cross-section. The magnitude of the current density at a point a distance r from the center of the wire is given by $J=J_0\frac{r}{R},$ where $J_0$ is a constant. Find the magnetic field (a) at a point outside the wire and (b) at a point inside the wire. Write your answer in terms of the net current I through the wire.

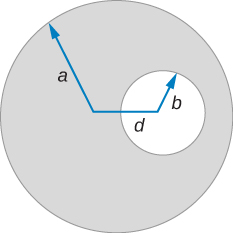
A very long, cylindrical wire of radius a has a circular hole of radius b in it at a distance d from the center. The wire carries a uniform current of magnitude I through it. The direction of the current in the figure is out of the paper. Find the magnetic field (a) at a point at the edge of the hole closest to the center of the thick wire, (b) at an arbitrary point inside the hole, and (c) at an arbitrary point outside the wire. ( Hint: Think of the hole as a sum of two wires carrying current in the opposite directions.)

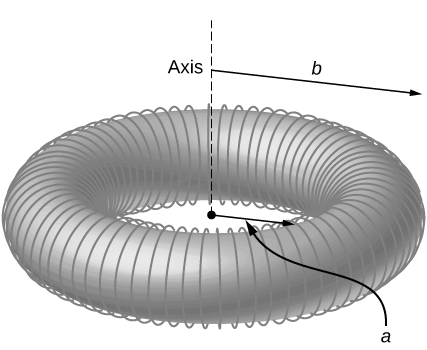
Magnetic field inside a torus. Consider a torus of rectangular cross-section with inner radius a and outer radius b . N turns of an insulated thin wire are wound evenly on the torus tightly all around the torus and connected to a battery producing a steady current I in the wire. Assume that the current on the top and bottom surfaces in the figure is radial, and the current on the inner and outer radii surfaces is vertical. Find the magnetic field inside the torus as a function of radial distance r from the axis.

Two long coaxial copper tubes, each of length L , are connected to a battery of voltage V . The inner tube has inner radius a and outer radius b , and the outer tube has inner radius c and outer radius d . The tubes are then disconnected from the battery and rotated in the same direction at angular speed of $\omega$ radians per second about their common axis. Find the magnetic field (a) at a point inside the space enclosed by the inner tube $r<a,$ and (b) at a point between the tubes $b<r<c,$ and (c) at a point outside the tubes $r>d.$ ( Hint: Think of copper tubes as a capacitor and find the charge density based on the voltage applied, $Q=VC,$ $C=\frac{2\pi {\epsilon }_{0}L}{\text{ln}\left(c\text{/}b\right)}\text{.)}$

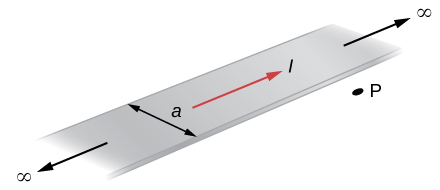
The accompanying figure shows a flat, infinitely long sheet of width a that carries a current I uniformly distributed across it. Find the magnetic field at the point P, which is in the plane of the sheet and at a distance x from one edge. Test your result for the limit $a\to 0.$

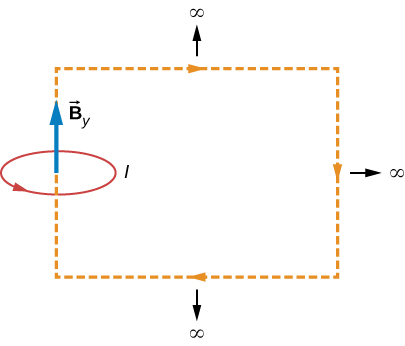
A hypothetical current flowing in the z -direction creates the field $\overrightarrow{B}=C\left[\left(x\text{/}{y}^2\right)\widehat{i}+\left(1\text{/}y\right)\widehat{j}\right]$ in the rectangular region of the xy -plane shown in the accompanying figure. Use Ampère’s law to find the current through the rectangle.

A nonconducting hard rubber circular disk of radius R is painted with a uniform surface charge density $\sigma .$ It is rotated about its axis with angular speed $\omega .$ (a) Find the magnetic field produced at a point on the axis a distance h meters from the center of the disk. (b) Find the numerical value of magnitude of the magnetic field when $\sigma =1{\text{C/m}}^2,$ $R=\text{20 cm},h=\text{2 cm},$ and $\omega =400\text{rad/sec},$ and compare it with the magnitude of magnetic field of Earth, which is about 1/2 Gauss.