7.5 Equipotential surfaces and conductors  (Page 12/9)

We can represent electric potentials (voltages) pictorially, just as we drew pictures to illustrate electric fields. This is not surprising, since the two concepts are related. Consider [link] , which shows an isolated positive point charge and its electric field lines, which radiate out from a positive charge and terminate on negative charges. We use blue arrows to represent the magnitude and direction of the electric field, and we use green lines to represent places where the electric potential is constant. These are called equipotential surface     s in three dimensions, or equipotential line     s in two dimensions. The term equipotential is also used as a noun, referring to an equipotential line or surface. The potential for a point charge is the same anywhere on an imaginary sphere of radius r surrounding the charge. This is true because the potential for a point charge is given by $V=kq\text{/}r$ and thus has the same value at any point that is a given distance r from the charge. An equipotential sphere is a circle in the two-dimensional view of [link] . Because the electric field lines point radially away from the charge, they are perpendicular to the equipotential lines.

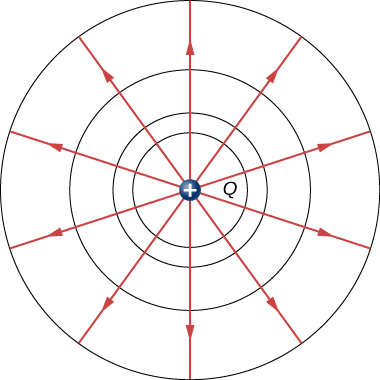
It is important to note that equipotential lines are always perpendicular to electric field lines . No work is required to move a charge along an equipotential, since $\text{Δ}V=0$ . Thus, the work is

Work is zero if the direction of the force is perpendicular to the displacement. Force is in the same direction as E , so motion along an equipotential must be perpendicular to E . More precisely, work is related to the electric field by

Note that in this equation, E and F symbolize the magnitudes of the electric field and force, respectively. Neither q nor E is zero; d is also not zero. So $\text{cos}\theta$ must be 0, meaning $\theta$ must be $90\text{º}$ . In other words, motion along an equipotential is perpendicular to E .

One of the rules for static electric fields and conductors is that the electric field must be perpendicular to the surface of any conductor. This implies that a conductor is an equipotential surface in static situations . There can be no voltage difference across the surface of a conductor, or charges will flow. One of the uses of this fact is that a conductor can be fixed at what we consider zero volts by connecting it to the earth with a good conductor—a process called grounding    . Grounding can be a useful safety tool. For example, grounding the metal case of an electrical appliance ensures that it is at zero volts relative to Earth.