7.1 Electric potential energy  (Page 109/5)

When a free positive charge q is accelerated by an electric field, it is given kinetic energy ( [link] ). The process is analogous to an object being accelerated by a gravitational field, as if the charge were going down an electrical hill where its electric potential energy is converted into kinetic energy, although of course the sources of the forces are very different. Let us explore the work done on a charge q by the electric field in this process, so that we may develop a definition of electric potential energy.

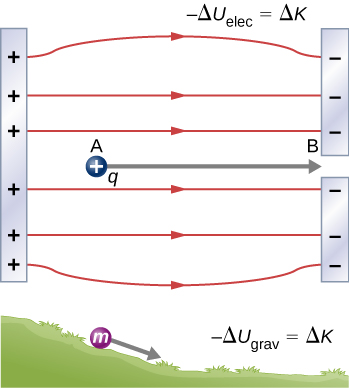
The electrostatic or Coulomb force is conservative, which means that the work done on q is independent of the path taken, as we will demonstrate later. This is exactly analogous to the gravitational force. When a force is conservative, it is possible to define a potential energy associated with the force. It is usually easier to work with the potential energy (because it depends only on position) than to calculate the work directly.

To show this explicitly, consider an electric charge $+q$ fixed at the origin and move another charge $+Q$ toward q in such a manner that, at each instant, the applied force $\overrightarrow{\text{F}}$ exactly balances the electric force ${\overrightarrow{\text{F}}}_e$ on Q ( [link] ). The work done by the applied force $\overrightarrow{\text{F}}$ on the charge Q changes the potential energy of Q . We call this potential energy the electrical potential energy of Q .

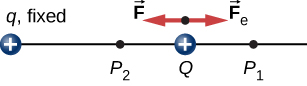
The work $W_{12}$ done by the applied force $\overrightarrow{\text{F}}$ when the particle moves from $P_1$ to $P_2$ may be calculated by

Since the applied force $\overrightarrow{\text{F}}$ balances the electric force ${\overrightarrow{\text{F}}}_e$ on Q , the two forces have equal magnitude and opposite directions. Therefore, the applied force is

where we have defined positive to be pointing away from the origin and r is the distance from the origin. The directions of both the displacement and the applied force in the system in [link] are parallel, and thus the work done on the system is positive.

We use the letter U to denote electric potential energy, which has units of joules (J). When a conservative force does negative work, the system gains potential energy. When a conservative force does positive work, the system loses potential energy, $\text{Δ}U=\text{−}W.$ In the system in [link] , the Coulomb force acts in the opposite direction to the displacement; therefore, the work is negative. However, we have increased the potential energy in the two-charge system.

Kinetic energy of a charged particle

A $+3.0\text{-nC}$ charge Q is initially at rest a distance of 10 cm ( $r_1$ ) from a $+5.0\text{-nC}$ charge q fixed at the origin ( [link] ). Naturally, the Coulomb force accelerates Q away from q , eventually reaching 15 cm ( $r_2$ ).

1. What is the work done by the electric field between $r_1$ and $r_2$ ?
2. How much kinetic energy does Q have at $r_2$ ?

Strategy

Calculate the work with the usual definition. Since Q started from rest, this is the same as the kinetic energy.

Solution

Integrating force over distance, we obtain

$\begin{array}{cc}{W}_{12}\hfill & ={\displaystyle {\int }_{r_1}^{r_2}\overrightarrow{\text{F}}·d\overrightarrow{\text{r}}}={\displaystyle {\int }_{r_1}^{r_2}\frac{kqQ}{r^2}dr={\left[-\frac{kqQ}{r}\right]}_{r_1}^{r_2}}=kqQ\left[\frac{\mathrm{-1}}{r_2}+\frac{1}{r_1}\right]\hfill \\ & =\left(8.99\times {10}^9{\text{Nm}}^2{\text{/C}}^2\right)\left(5.0\times {10}^{\mathrm{-9}}\text{C}\right)\left(3.0\times {10}^{\mathrm{-9}}\text{C}\right)\left[\frac{\mathrm{-1}}{0.15\text{m}}+\frac{1}{0.10\text{m}}\right]\hfill \\ & =4.5\times {10}^{\mathrm{-7}}\text{J}\text{.}\hfill \end{array}$

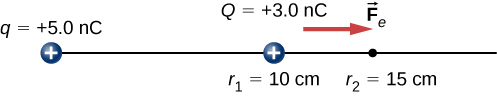
This is also the value of the kinetic energy at $r_2.$

Significance

Charge Q was initially at rest; the electric field of q did work on Q , so now Q has kinetic energy equal to the work done by the electric field.

Got questions? Get instant answers now!