| << Chapter < Page | Chapter >> Page > |
When an ideal gas is compressed adiabatically work is done on it and its temperature increases; in an adiabatic expansion , the gas does work and its temperature drops. Adiabatic compressions actually occur in the cylinders of a car, where the compressions of the gas-air mixture take place so quickly that there is no time for the mixture to exchange heat with its environment. Nevertheless, because work is done on the mixture during the compression, its temperature does rise significantly. In fact, the temperature increases can be so large that the mixture can explode without the addition of a spark. Such explosions, since they are not timed, make a car run poorly—it usually “knocks.” Because ignition temperature rises with the octane of gasoline, one way to overcome this problem is to use a higher-octane gasoline.
Another interesting adiabatic process is the free expansion of a gas. [link] shows a gas confined by a membrane to one side of a two-compartment, thermally insulated container. When the membrane is punctured, gas rushes into the empty side of the container, thereby expanding freely. Because the gas expands “against a vacuum” , it does no work, and because the vessel is thermally insulated, the expansion is adiabatic. With and in the first law, so for the free expansion.
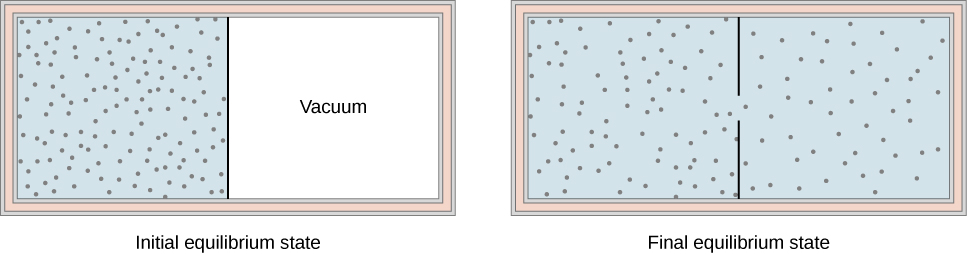
If the gas is ideal, the internal energy depends only on the temperature. Therefore, when an ideal gas expands freely, its temperature does not change.
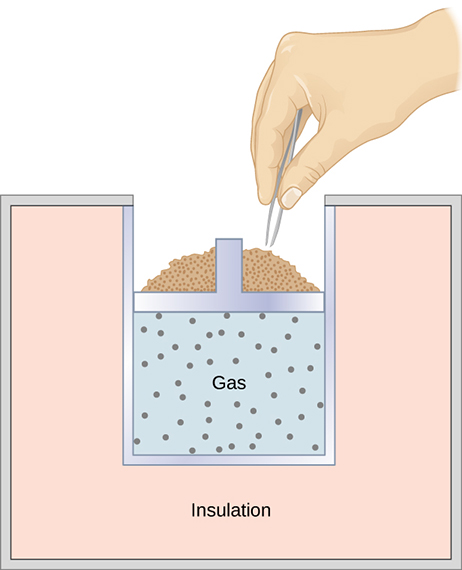
A quasi-static, adiabatic expansion of an ideal gas is represented in [link] , which shows an insulated cylinder that contains 1 mol of an ideal gas. The gas is made to expand quasi-statically by removing one grain of sand at a time from the top of the piston. When the gas expands by dV , the change in its temperature is dT . The work done by the gas in the expansion is because the cylinder is insulated; and the change in the internal energy of the gas is, from [link] , Therefore, from the first law,
so
Also, for 1 mol of an ideal gas,
so
and
We now have two equations for dT . Upon equating them, we find that
Now, we divide this equation by pV and use . We are then left with
which becomes
where we define as the ratio of the molar heat capacities:
Thus,
and
Finally, using , we can write this in the form
This equation is the condition that must be obeyed by an ideal gas in a quasi-static adiabatic process. For example, if an ideal gas makes a quasi-static adiabatic transition from a state with pressure and volume and to a state with and then it must be true that

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?