| << Chapter < Page | Chapter >> Page > |
We have just seen that some circuits may be analyzed by reducing a circuit to a single voltage source and an equivalent resistance. Many complex circuits cannot be analyzed with the series-parallel techniques developed in the preceding sections. In this section, we elaborate on the use of Kirchhoff’s rules to analyze more complex circuits. For example, the circuit in [link] is known as a multi-loop circuit , which consists of junctions. A junction, also known as a node, is a connection of three or more wires. In this circuit, the previous methods cannot be used, because not all the resistors are in clear series or parallel configurations that can be reduced. Give it a try. The resistors and are in series and can be reduced to an equivalent resistance. The same is true of resistors and . But what do you do then?
Even though this circuit cannot be analyzed using the methods already learned, two circuit analysis rules can be used to analyze any circuit, simple or complex. The rules are known as Kirchhoff’s rules , after their inventor Gustav Kirchhoff (1824–1887).
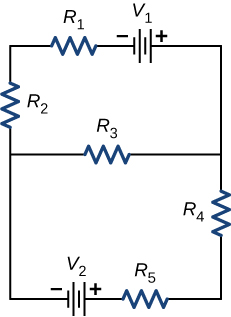
We now provide explanations of these two rules, followed by problem-solving hints for applying them and a worked example that uses them.
Kirchhoff’s first rule (the junction rule ) applies to the charge entering and leaving a junction ( [link] ). As stated earlier, a junction, or node, is a connection of three or more wires. Current is the flow of charge, and charge is conserved; thus, whatever charge flows into the junction must flow out.
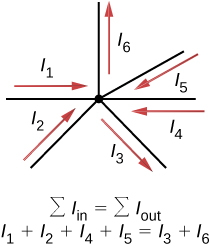
Although it is an over-simplification, an analogy can be made with water pipes connected in a plumbing junction. If the wires in [link] were replaced by water pipes, and the water was assumed to be incompressible, the volume of water flowing into the junction must equal the volume of water flowing out of the junction.
Kirchhoff’s second rule (the loop rule ) applies to potential differences. The loop rule is stated in terms of potential V rather than potential energy, but the two are related since In a closed loop, whatever energy is supplied by a voltage source, the energy must be transferred into other forms by the devices in the loop, since there are no other ways in which energy can be transferred into or out of the circuit. Kirchhoff’s loop rule states that the algebraic sum of potential differences, including voltage supplied by the voltage sources and resistive elements, in any loop must be equal to zero. For example, consider a simple loop with no junctions, as in [link] .

Notification Switch
Would you like to follow the 'University physics volume 2' conversation and receive update notifications?