| << Chapter < Page | Chapter >> Page > |
One very important example of electric fields which is used extensively is the electric field between two charged parallelplates. In this situation the electric field is constant. This is used for many practical purposes and later we will explain howMillikan used it to measure the charge on the electron.
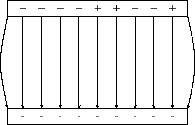
This means that the force that a test charge would feel at any point between the plates would be identical in magnitude anddirection. The fields on the edges exhibit fringe effects, i.e. they bulge outwards . This is because a test charge placed here would feel the effects of charges only on one side(either left or right depending on which side it is placed). Test charges placed in the middle experience the effects of charges onboth sides so they balance the components in the horizontal direction. This is clearly not the case on the edges.
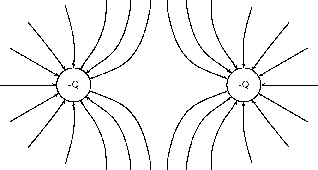
When we started making field maps we drew arrows to indicate the strength of the field and the direction. When we moved to linesyou might have asked “Did we forget about the field strength?”. We did not. Consider the case for a single positive charge again:
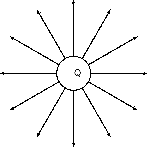
Notice that as you move further away from the charge the field lines become more spread out. In field map diagrams, the closer togetherfield lines are, the stronger the field. Therefore, the electric field is stronger closer to the charge (the electric field lines are closer together) and weaker further from the charge (the electric field lines are further apart).
The magnitude of the electric field at a point as the force per unit charge. Therefore,
E and F are vectors. From this we see that the force on a charge is simply:
The force between two electric charges is given by:
(if we make the one charge and the other .) Therefore, the electric field can be written as:
The electric field is the force per unit of charge and hence has units of newtons per coulomb.
As with Coulomb's law calculations, do not substitute the sign of the charge into the equation for electric field. Instead, choose apositive direction, and then either add or subtract the contribution to the electric field due to each charge dependingupon whether it points in the positive or negative direction, respectively.
Khan academy video on electrostatics - 2
Phet simulation for electric fields
Calculate the electric field strength from a charge.
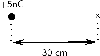
We need to calculate the electric field a distance from a given charge.
We are given the magnitude of the charge and the distance from the charge.
We will use the equation:
Two charges of = and = are separated by a distance of . What is the electric field strength at a point that is from and from ? The point lies beween and .

We need to calculate the electric field a distance from two given charges.
We are given the magnitude of the charges and the distances from the charges.
We will use the equation:
We need to work out the electric field for each charge separately and then add them to get the resultant field.
We first solve for :
Then for :
We need to add the two electric fields beacuse both are in the same direction. The field is away from and towards . Therefore,

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 11 physical science' conversation and receive update notifications?