18.1 Resistance (Page 19/2)

Siyavula textbooks: grade 11 Page 1 / 2

Resistance

In Grade 10, you learnt about resistors and were introduced to circuits where resistors were connected in series and circuits where resistors were connected in parallel. In a series circuit there is one path for the current to flow through. In a parallel circuit there are multiple paths for the current to flow through.

Equivalent resistance

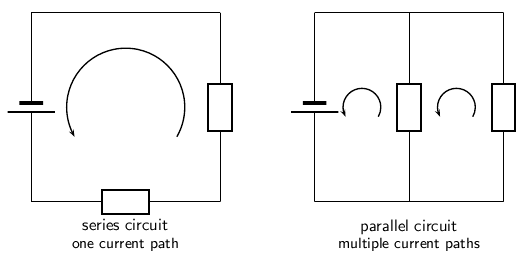
When there is more than one resistor in a circuit, we are usually able to calculate the total combined resitance of all the resistors. The resistance of the single resistor is known as equivalent resistance .

Equivalent series resistance

Consider a circuit consisting of three resistors and a single cell connected in series.

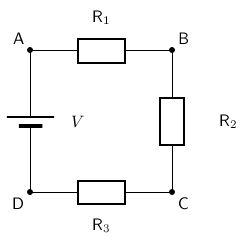
The first principle to understand about series circuits is that the amount of current is the same through any component in the circuit. This is because there is only one path for electrons to flow in a series circuit. From the way that the battery is connected, we can tell which direction the current will flow. We know that current flows from positive to negative, by convention. Current in this circuit will flow in a clockwise direction, from point A to B to C to D and back to A.

So, how do we use this knowledge to calculate the total resistance in the circuit?

We know that in a series circuit the current has to be the same in all components. So we can write:

I = I_{1} = I_{2} = I_{3}

We also know that total voltage of the circuit has to be equal to the sum of the voltages over all three resistors. So we can write:

V = V_{1} + V_{2} + V_{3}

Finally, we know that Ohm's Law has to apply for each resistor individually, which gives us:

\begin{matrix} V_{1} & = & I_{1} \cdot R_{1} \\ V_{2} & = & I_{2} \cdot R_{2} \\ V_{3} & = & I_{3} \cdot R_{3} \end{matrix}

Therefore:

V = I_{1} \cdot R_{1} + I_{2} \cdot R_{2} + I_{3} \cdot R_{3}

However, because

I = I_{1} = I_{2} = I_{3}

, we can further simplify this to:

\begin{matrix} V & = & I \cdot R_{1} + I \cdot R_{2} + I \cdot R_{3} \\ = & I (R_{1} + R_{2} + R_{3}) \end{matrix}

Further, we can write an Ohm's Law relation for the entire circuit:

V = I \cdot R

Therefore:

\begin{matrix} V & = & I (R_{1} + R_{2} + R_{3}) \\ I \cdot R & = & I (R_{1} + R_{2} + R_{3}) \\ ∴ R & = & R_{1} + R_{2} + R_{3} \end{matrix}

Equivalent resistance in a series circuit,

R_{s}

For $n$ resistors in series the equivalent resistance is:

R_{s} = R_{1} + R_{2} + R_{3} + \dots + R_{n}

You can use the following simulation to test this result and all other results in this chapter.

run demo

Let us apply this to the following circuit.

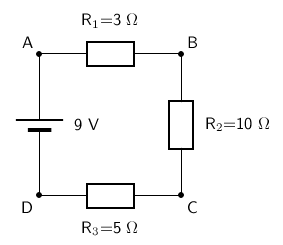
The resistors are in series, therefore:

\begin{matrix} R_{s} & = & R_{1} + R_{2} + R_{3} \\ = & 3 Ω + 10 Ω + 5 Ω \\ = & 18 Ω \end{matrix}

Khan academy video on electric circuits - 1

Two 10 k $Ω$ resistors are connected in series. Calculate the equivalent resistance.

Determine how to approach the problem
Since the resistors are in series we can use:

$R_{s} = R_{1} + R_{2}$
Solve the problem
$\begin{matrix} R_{s} & = & R_{1} + R_{2} \\ = & 10 k Ω + 10 k Ω \\ = & 20 k Ω \end{matrix}$
Write the final answer
The equivalent resistance of two 10 k $Ω$ resistors connected in series is 20 k $Ω$ .

Got questions? Get instant answers now!

Two resistors are connected in series. The equivalent resistance is 100 $Ω$ . If one resistor is 10 $Ω$ , calculate the value of the second resistor.

Determine how to approach the problem
Since the resistors are in series we can use:

$R_{s} = R_{1} + R_{2}$

We are given the value of $R_{s}$ and $R_{1}$ .
Solve the problem
$\begin{matrix} R_{s} & = & R_{1} + R_{2} \\ ∴ R_{2} & = & R_{s} - R_{1} \\ = & 100 Ω - 10 Ω \\ = & 90 Ω \end{matrix}$
Write the final answer
The second resistor has a resistance of 90 $Ω$ .

Got questions? Get instant answers now!

Equivalent parallel resistance

Consider a circuit consisting of a single cell and three resistors that are connected in parallel.

<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Siyavula textbooks: grade 11 physical science. OpenStax CNX. Jul 29, 2011 Download for free at http://cnx.org/content/col11241/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Siyavula textbooks: grade 11 physical science' conversation and receive update notifications?

Ask

©flickr: quinn	Neuroanatomy By George Turner Start Quiz
©flickr: Abraham	2 Biology 2 By Sarah Warren Start Test
	5 Physiotherapy Flashcards Set 5 By Rhodes Start Flashcards
	20 Hemostasis Dr. Olver By Brooke Delaney Start Exam
	Statistics Final Review By Madison Christian Start Exam
	13 Lec:13 Hypothesis Testing P-values By Janet Forrester Start Quiz
	Anthropology Politics Culture By Richley Crapo Start Assignment
©flickr:	Morphology By Jugnu Khan Start Quiz
	6 Biology 06 Metabolism MCQ By OpenStax Start Quiz
	4 Microeconomics 04 Labor Financial Markets By OpenStax Start Flashcards