| << Chapter < Page | Chapter >> Page > |
A man is pulling a 20 kg box with a rope that makes an angle of 60 with the horizontal. If he applies a force of 150 N and a frictional force of 15 N is present, calculate the acceleration of the box.
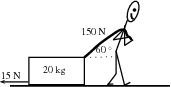
The motion is horizontal and therefore we will only consider the forces in a horizontal direction. Remember that vertical forces do not influence horizontal motion and vice versa.
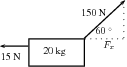
The applied force is acting at an angle of 60 to the horizontal. We can only consider forces that are parallel to the motion. The horizontal component of the applied force needs to be calculated before we can continue:
To find the acceleration we apply Newton's Second Law:
A 2000 kg truck pulls a 500 kg trailer with a constant acceleration. The engine of the truck produces a thrust of 10 000 N. Ignore the effect of friction.
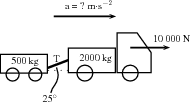
Draw a force diagram indicating all the horizontal forces on the system as a whole:
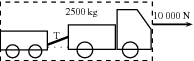
In the absence of friction, the only force that causes the system to accelerate is the thrust of the engine. If we now apply Newton's Second Law:
We are asked to find the tension in the tow bar, but because the tow bar is acting at an angle, we need to find the horizontal component first. We will find the horizontal component in terms of T and then use it in the next step to find T.
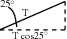
The horizontal component is T cos 25 .
To find T, we will apply Newton's Second Law:
When we place an object on a slope the force of gravity (F ) acts straight down and not perpendicular to the slope. Due to gravity pulling straight down, the object will tend to slide down the slope with a force equal to the horizontal component of the force of gravity (F sin ). The object will 'stick' to the slope due to the frictional force between the object and the surface. As you increase the angle of the slope, the horizontal component will also increase until the frictional force is overcome and the object starts to slide down the slope.
The force of gravity will also tend to push an object 'into' the slope. The vertical component of this force is equal to the vertical component of the force of gravity (F cos ). There is no movement in this direction as this force is balanced by the slope pushing up against the object. This “pushing force” is called the normal force (N) and is equal to the force required to make the component of the resultant force perpendicularly into the plane zero, F cos in this case, but opposite in direction.

A body of mass M is at rest on an inclined plane.
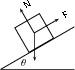
What is the magnitude of the frictional force acting on the body?
The question asks us to identify the frictional force. The body is said to be at rest on the plane, which means that it is not moving and therefore there is no resultant force. The frictional force must therefore be balanced by the force F up the inclined plane.
The frictional force is equal to the component of the weight (Mg) parallel to the surface, which is equal to Mg sin .
A force T = 312 N is required to keep a body at rest on a frictionless inclined plane which makes an angle of 35 with the horizontal. The forces acting on the body are shown. Calculate the magnitudes of forces P and R, giving your answers to three significant figures.
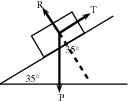
We are usually asked to find the magnitude of T, but in this case T is given and we are asked to find P. We can use the same equation. T is the force that balances the component of P parallel to the plane (P ) and therefore it has the same magnitude.
R can also be determined with the use of trigonometric ratios. The tan or cos ratio can be used. We recommend that you use the tan ratio because it does not involve using the value for P (for in case you made a mistake in calculating P).
Note that the question asks that the answers be given to 3 significant figures. We therefore round 445,6 N up to 446 N.

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 11 physical science' conversation and receive update notifications?