1. Home
  2. Siyavula textbooks: grade 11
  3. Vectors
  4. Adding and subtracting vectors

10.2 Adding and subtracting vectors  (Page 3/4)

<< Chapter < Page
  Siyavula textbooks: grade 11     Page 3 / 4
Chapter >> Page >

The parallelogram method is restricted to the addition of just two vectors. However, it is arguably the most intuitive way of adding twoforces acting on a point.

Algebraic addition and subtraction of vectors

Vectors in a straight line

Whenever you are faced with adding vectors acting in a straight line (i.e. some directed left and some right, or some acting up and others down) you can use a very simple algebraic technique:

Method: Addition/Subtraction of Vectors in a Straight Line

  1. Choose a positive direction. As an example, for situations involving displacements in the directions west and east, youmight choose west as your positive direction. In that case, displacements east are negative.
  2. Next simply add (or subtract) themagnitude of the vectors using the appropriate signs.
  3. As a final step the direction of the resultant should be included in words (positive answers are in the positive direction, while negativeresultants are in the negative direction).

Let us consider a few examples.

A tennis ball is rolled towards a wall which is 10 m away from the ball. If after striking the wall the ball rolls a further 2,5 m along the ground away from the wall, calculate algebraically the ball's resultant displacement.

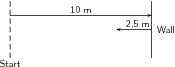
  2. We know that the resultant displacement of the ball ( x → R ) is equal to the sum of the ball's separate displacements ( x → 1 and x → 2 ):

    x → R = x → 1 + x → 2

    Since the motion of the ball is in a straight line (i.e. the ball moves towards and away from the wall), we can use the method of algebraic additionjust explained.

  3. Let's choose the positive direction to be towards the wall. This means that the negative direction is away from the wall.

  4. With right positive:

    x → 1 = + 10 , 0 m · s - 1 x → 2 = - 2 , 5 m · s - 1

  5. Next we simply add the two displacements to give the resultant:

    x → R = ( + 10 m · s - 1 ) + ( - 2 , 5 m · s - 1 ) = ( + 7 , 5 ) m · s - 1

  6. Finally, in this case towards the wall is the positive direction , so: x → R = 7,5 m towards the wall.

Got questions? Get instant answers now!

Suppose that a tennis ball is thrown horizontally towards a wall at an initial velocity of 3 m · s - 1 to the right. After striking the wall, the ball returns to the thrower at 2 m · s - 1 . Determine the change in velocity of the ball.

  1. A quick sketch will help us understand the problem.

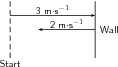
  2. Remember that velocity is a vector. The change in the velocity of the ball is equal to the difference between the ball's initial and finalvelocities:

    Δ v → = v → f - v → i

    Since the ball moves along a straight line (i.e. left and right), we can use the algebraic technique of vector subtraction just discussed.

  3. Choose the positive direction to be towards the wall. This means that the negative direction is away from the wall.

  4. v → i = + 3 m · s - 1 v → f = - 2 m · s - 1

  5. Thus, the change in velocity of the ball is:

    Δ v → = ( - 2 m · s - 1 ) - ( + 3 m · s - 1 ) = ( - 5 ) m · s - 1

  6. Remember that in this case towards the wall means a positive velocity , so away from the wall means a negative velocity : Δ v → = 5 m · s - 1 away from the wall.

Got questions? Get instant answers now!
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Siyavula textbooks: grade 11 physical science. OpenStax CNX. Jul 29, 2011 Download for free at http://cnx.org/content/col11241/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Siyavula textbooks: grade 11 physical science' conversation and receive update notifications?

Ask