| << Chapter < Page | Chapter >> Page > |
Kepler’s third law states that the square of the period is proportional to the cube of the semi-major axis of the orbit. In Satellite Orbits and Energy , we derived Kepler’s third law for the special case of a circular orbit. [link] gives us the period of a circular orbit of radius r about Earth:
For an ellipse, recall that the semi-major axis is one-half the sum of the perihelion and the aphelion. For a circular orbit, the semi-major axis ( a ) is the same as the radius for the orbit. In fact, [link] gives us Kepler’s third law if we simply replace r with a and square both sides.
We have changed the mass of Earth to the more general M , since this equation applies to satellites orbiting any large mass.
This yields a value of or 17.8 AU for the semi-major axis.
The semi-major axis is one-half the sum of the aphelion and perihelion, so we have
Substituting for the values, we found for the semi-major axis and the value given for the perihelion, we find the value of the aphelion to be 35.0 AU.
Check Your Understanding The nearly circular orbit of Saturn has an average radius of about 9.5 AU and has a period of 30 years, whereas Uranus averages about 19 AU and has a period of 84 years. Is this consistent with our results for Halley’s comet?
The semi-major axis for the highly elliptical orbit of Halley’s comet is 17.8 AU and is the average of the perihelion and aphelion. This lies between the 9.5 AU and 19 AU orbital radii for Saturn and Uranus, respectively. The radius for a circular orbit is the same as the semi-major axis, and since the period increases with an increase of the semi-major axis, the fact that Halley’s period is between the periods of Saturn and Uranus is expected.
Are Kepler’s laws purely descriptive, or do they contain causal information?
In the diagram below for a satellite in an elliptical orbit about a much larger mass, indicate where its speed is the greatest and where it is the least. What conservation law dictates this behavior? Indicate the directions of the force, acceleration, and velocity at these points. Draw vectors for these same three quantities at the two points where the y -axis intersects (along the semi-minor axis) and from this determine whether the speed is increasing decreasing, or at a max/min.
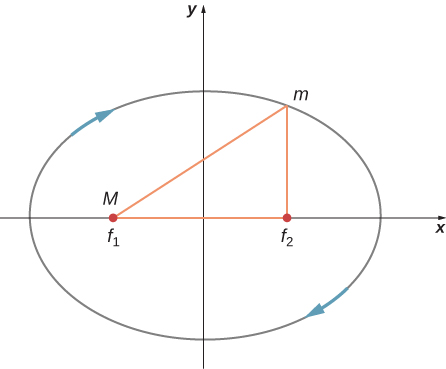
The speed is greatest where the satellite is closest to the large mass and least where farther away—at the periapsis and apoapsis, respectively. It is conservation of angular momentum that governs this relationship. But it can also be gleaned from conservation of energy, the kinetic energy must be greatest where the gravitational potential energy is the least (most negative). The force, and hence acceleration, is always directed towards M in the diagram, and the velocity is always tangent to the path at all points. The acceleration vector has a tangential component along the direction of the velocity at the upper location on the y -axis; hence, the satellite is speeding up. Just the opposite is true at the lower position.
Calculate the mass of the Sun based on data for average Earth’s orbit and compare the value obtained with the Sun’s commonly listed value of .
; The values are the same within 0.05%.
Io orbits Jupiter with an average radius of 421,700 km and a period of 1.769 days. Based upon these data, what is the mass of Jupiter?
The “mean” orbital radius listed for astronomical objects orbiting the Sun is typically not an integrated average but is calculated such that it gives the correct period when applied to the equation for circular orbits. Given that, what is the mean orbital radius in terms of aphelion and perihelion?
Compare [link] and [link] to see that they differ only in that the circular radius, r , is replaced by the semi-major axis, a . Therefore, the mean radius is one-half the sum of the aphelion and perihelion, the same as the semi-major axis.
The perihelion of Halley’s comet is 0.586 AU and the aphelion is 17.8 AU. Given that its speed at perihelion is 55 km/s, what is the speed at aphelion ( )? ( Hint: You may use either conservation of energy or angular momentum, but the latter is much easier.)
The perihelion of the comet Lagerkvist is 2.61 AU and it has a period of 7.36 years. Show that the aphelion for this comet is 4.95 AU.
The semi-major axis, 3.78 AU is found from the equation for the period. This is one-half the sum of the aphelion and perihelion, giving an aphelion distance of 4.95 AU.
What is the ratio of the speed at perihelion to that at aphelion for the comet Lagerkvist in the previous problem?
Eros has an elliptical orbit about the Sun, with a perihelion distance of 1.13 AU and aphelion distance of 1.78 AU. What is the period of its orbit?
1.75 years

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?