| << Chapter < Page | Chapter >> Page > |
The angular frequency for damped harmonic motion becomes
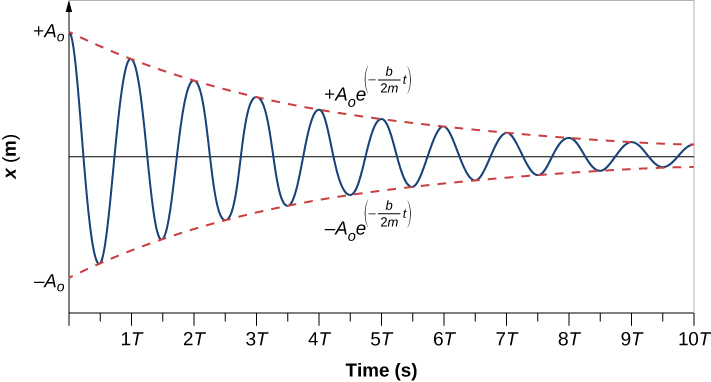
Recall that when we began this description of damped harmonic motion, we stated that the damping must be small. Two questions come to mind. Why must the damping be small? And how small is small? If you gradually increase the amount of damping in a system, the period and frequency begin to be affected, because damping opposes and hence slows the back and forth motion. (The net force is smaller in both directions.) If there is very large damping, the system does not even oscillate—it slowly moves toward equilibrium. The angular frequency is equal to
As b increases, becomes smaller and eventually reaches zero when . If b becomes any larger, becomes a negative number and is a complex number.
[link] shows the displacement of a harmonic oscillator for different amounts of damping. When the damping constant is small, , the system oscillates while the amplitude of the motion decays exponentially. This system is said to be underdamped , as in curve (a). Many systems are underdamped, and oscillate while the amplitude decreases exponentially, such as the mass oscillating on a spring. The damping may be quite small, but eventually the mass comes to rest. If the damping constant is , the system is said to be critically damped , as in curve (b). An example of a critically damped system is the shock absorbers in a car. It is advantageous to have the oscillations decay as fast as possible. Here, the system does not oscillate, but asymptotically approaches the equilibrium condition as quickly as possible. Curve (c) in [link] represents an overdamped system where An overdamped system will approach equilibrium over a longer period of time.
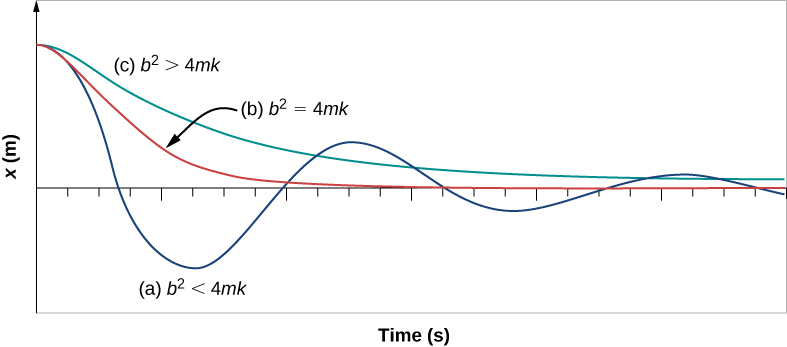
Critical damping is often desired, because such a system returns to equilibrium rapidly and remains at equilibrium as well. In addition, a constant force applied to a critically damped system moves the system to a new equilibrium position in the shortest time possible without overshooting or oscillating about the new position.
Check Your Understanding Why are completely undamped harmonic oscillators so rare?
Friction often comes into play whenever an object is moving. Friction causes damping in a harmonic oscillator.
Give an example of a damped harmonic oscillator. (They are more common than undamped or simple harmonic oscillators.)
A car shock absorber.
How would a car bounce after a bump under each of these conditions?
(a) overdamping
(b) underdamping
(c) critical damping
Most harmonic oscillators are damped and, if undriven, eventually come to a stop. Why?
The second law of thermodynamics states that perpetual motion machines are impossible. Eventually the ordered motion of the system decreases and returns to equilibrium.
The amplitude of a lightly damped oscillator decreases by during each cycle. What percentage of the mechanical energy of the oscillator is lost in each cycle?
9%

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?