| << Chapter < Page | Chapter >> Page > |
Kepler’s second law states that a planet sweeps out equal areas in equal times, that is, the area divided by time, called the areal velocity, is constant. Consider [link] . The time it takes a planet to move from position A to B , sweeping out area , is exactly the time taken to move from position C to D , sweeping area , and to move from E to F , sweeping out area . These areas are the same: .
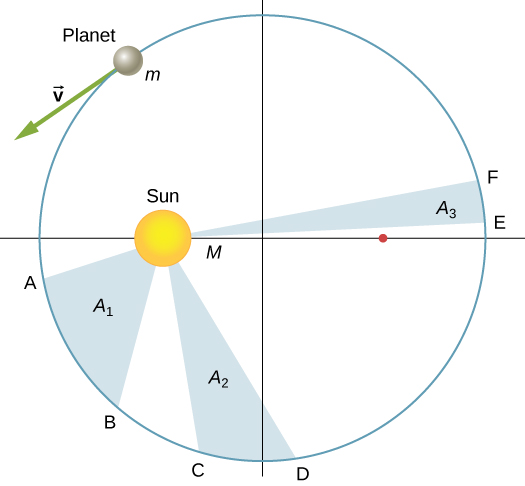
Comparing the areas in the figure and the distance traveled along the ellipse in each case, we can see that in order for the areas to be equal, the planet must speed up as it gets closer to the Sun and slow down as it moves away. This behavior is completely consistent with our conservation equation, [link] . But we will show that Kepler’s second law is actually a consequence of the conservation of angular momentum, which holds for any system with only radial forces.
Recall the definition of angular momentum from Angular Momentum , . For the case of orbiting motion, is the angular momentum of the planet about the Sun, is the position vector of the planet measured from the Sun, and is the instantaneous linear momentum at any point in the orbit. Since the planet moves along the ellipse, is always tangent to the ellipse.
We can resolve the linear momentum into two components: a radial component along the line to the Sun, and a component perpendicular to . The cross product for angular momentum can then be written as
.
The first term on the right is zero because is parallel to , and in the second term is perpendicular to , so the magnitude of the cross product reduces to . Note that the angular momentum does not depend upon . Since the gravitational force is only in the radial direction, it can change only and not ; hence, the angular momentum must remain constant.
Now consider [link] . A small triangular area is swept out in time . The velocity is along the path and it makes an angle with the radial direction. Hence, the perpendicular velocity is given by . The planet moves a distance projected along the direction perpendicular to r . Since the area of a triangle is one-half the base ( r ) times the height , for a small displacement, the area is given by . Substituting for , multiplying by m in the numerator and denominator, and rearranging, we obtain
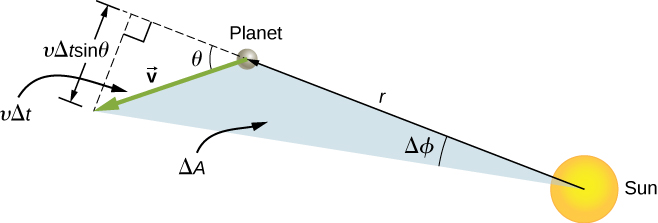
The areal velocity is simply the rate of change of area with time, so we have
Since the angular momentum is constant, the areal velocity must also be constant. This is exactly Kepler’s second law. As with Kepler’s first law, Newton showed it was a natural consequence of his law of gravitation.
You can view an animated version of [link] , and many other interesting animations as well, at the School of Physics (University of New South Wales) site.

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?