1. Home
  2. University physics volume 1
  3. Unit 1. mechanics
  4. Motion in two and three dimensions
  5. Acceleration vector

4.2 Acceleration vector  (Page 2/4)

<< Chapter < Page
  University physics volume 1     Page 2 / 4
Chapter >> Page >
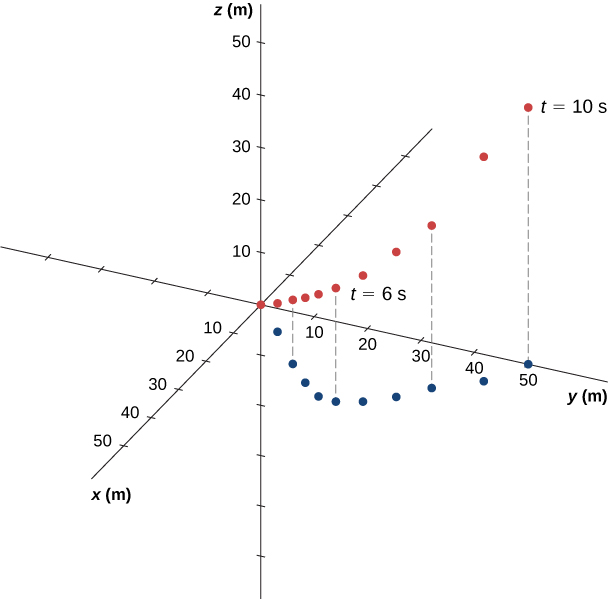
An x y z coordinate system is shown. All the axes show distance in meters and run from -50 to 50 meters. A series of 10 red dots are shown, with the sixth dot is labeled as t = 6 s and the tenth as t = 10 s. The red series of dots starts at the origin and curves upward (both y and z increasing with time). Vertical dashed lines connect the red dots to a series of blue dots in the x y plane. The blue dots are all in the first quadrant (positive x and y). The dots are regularly spaced along the y coordinate, while the x coordinate starts at 0, increases, reaches a maximum of x = 25 m at t = 5, and then decreases back to x = 0 at t 10 s.
The particle starts at point ( x , y , z ) = (0, 0, 0) with position vector r → = 0 . The projection of the trajectory onto the xy- plane is shown. The values of y and z increase linearly as a function of time, whereas x has a turning point at t = 5 s and 25 m, when it reverses direction. At this point, the x component of the velocity becomes negative. At t = 10 s, the particle is back to 0 m in the x direction.

Significance

By graphing the trajectory of the particle, we can better understand its motion, given by the numerical results of the kinematic equations.

Check Your Understanding Suppose the acceleration function has the form a → ( t ) = a i ^ + b j ^ + c k ^ m/ s 2 , where a, b, and c are constants. What can be said about the functional form of the velocity function?

The acceleration vector is constant and doesn’t change with time. If a, b , and c are not zero, then the velocity function must be linear in time. We have v → ( t ) = ∫ a → d t = ∫ ( a i ^ + b j ^ + c k ^ ) d t = ( a i ^ + b j ^ + c k ^ ) t m/s , since taking the derivative of the velocity function produces a → ( t ) . If any of the components of the acceleration are zero, then that component of the velocity would be a constant.

Got questions? Get instant answers now!

Constant acceleration

Multidimensional motion with constant acceleration can be treated the same way as shown in the previous chapter for one-dimensional motion. Earlier we showed that three-dimensional motion is equivalent to three one-dimensional motions, each along an axis perpendicular to the others. To develop the relevant equations in each direction, let’s consider the two-dimensional problem of a particle moving in the xy plane with constant acceleration, ignoring the z -component for the moment. The acceleration vector is

a → = a 0 x i ^ + a 0 y j ^ .

Each component of the motion has a separate set of equations similar to [link] – [link] of the previous chapter on one-dimensional motion. We show only the equations for position and velocity in the x - and y -directions. A similar set of kinematic equations could be written for motion in the z -direction:

x ( t ) = x 0 + ( v x ) avg t
v x ( t ) = v 0 x + a x t
x ( t ) = x 0 + v 0 x t + 1 2 a x t 2
v x 2 ( t ) = v 0 x 2 + 2 a x ( x − x 0 )
y ( t ) = y 0 + ( v y ) avg t
v y ( t ) = v 0 y + a y t
y ( t ) = y 0 + v 0 y t + 1 2 a y t 2
v y 2 ( t ) = v 0 y 2 + 2 a y ( y − y 0 ) .

Here the subscript 0 denotes the initial position or velocity. [link] to [link] can be substituted into [link] and [link] without the z -component to obtain the position vector and velocity vector as a function of time in two dimensions:

r → ( t ) = x ( t ) i ^ + y ( t ) j ^ and v → ( t ) = v x ( t ) i ^ + v y ( t ) j ^ .

The following example illustrates a practical use of the kinematic equations in two dimensions.

A skier

[link] shows a skier moving with an acceleration of 2.1 m/ s 2 down a slope of 15 ° at t = 0. With the origin of the coordinate system at the front of the lodge, her initial position and velocity are

r → ( 0 ) = ( 75.0 i ^ − 50.0 j ^ ) m

and

v → ( 0 ) = ( 4.1 i ^ − 1.1 j ^ ) m/s .

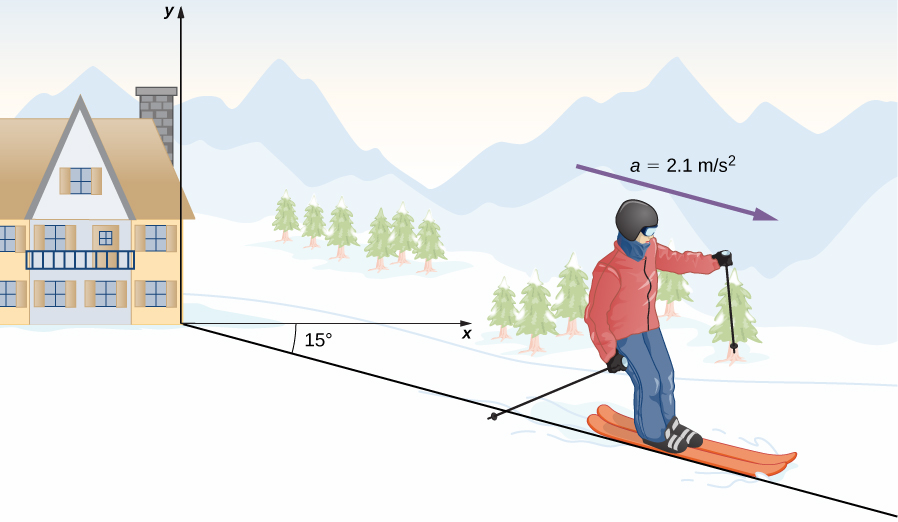
(a) What are the x- and y -components of the skier’s position and velocity as functions of time? (b) What are her position and velocity at t = 10.0 s?

An illustration of a skier in an x y coordinate system is shown. The skier is moving along a line that is 15 degrees below the horizontal x direction and has an acceleration of a = 2.1 meters per second squared also directed in his direction of motion. The acceleration is represented as a purple arrow.
A skier has an acceleration of 2.1 m/s 2 down a slope of 15 ° . The origin of the coordinate system is at the ski lodge.

Strategy

Since we are evaluating the components of the motion equations in the x and y directions, we need to find the components of the acceleration and put them into the kinematic equations. The components of the acceleration are found by referring to the coordinate system in [link] . Then, by inserting the components of the initial position and velocity into the motion equations, we can solve for her position and velocity at a later time t .
<< Chapter < Page Page > Chapter >>
Practice Key Terms 1

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, University physics volume 1. OpenStax CNX. Sep 19, 2016 Download for free at http://cnx.org/content/col12031/1.5
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'University physics volume 1' conversation and receive update notifications?

Ask