13.5 Kepler's laws of planetary motion  (Page 39/10)

Using the precise data collected by Tycho Brahe, Johannes Kepler carefully analyzed the positions in the sky of all the known planets and the Moon, plotting their positions at regular intervals of time. From this analysis, he formulated three laws, which we address in this section.

Kepler’s first law

The prevailing view during the time of Kepler was that all planetary orbits were circular. The data for Mars presented the greatest challenge to this view and that eventually encouraged Kepler to give up the popular idea. Kepler’s first law    states that every planet moves along an ellipse, with the Sun located at a focus of the ellipse. An ellipse is defined as the set of all points such that the sum of the distance from each point to two foci is a constant. [link] shows an ellipse and describes a simple way to create it.

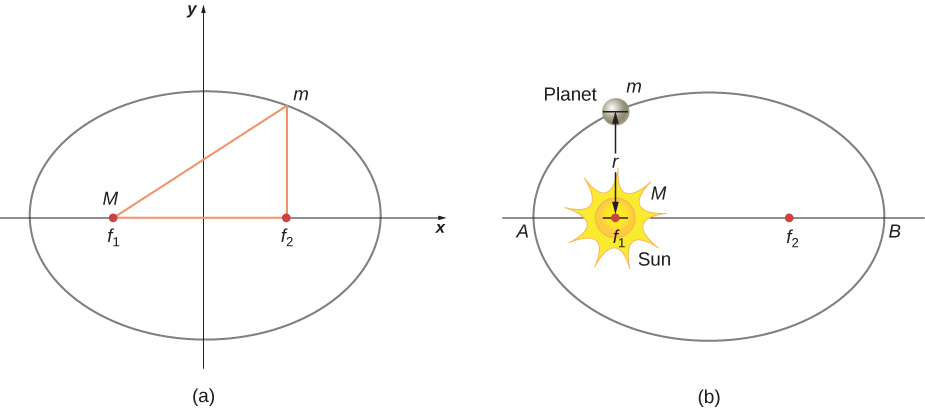
For elliptical orbits, the point of closest approach of a planet to the Sun is called the perihelion    . It is labeled point A in [link] . The farthest point is the aphelion    and is labeled point B in the figure. For the Moon’s orbit about Earth, those points are called the perigee and apogee, respectively.

An ellipse has several mathematical forms, but all are a specific case of the more general equation for conic sections. There are four different conic sections, all given by the equation

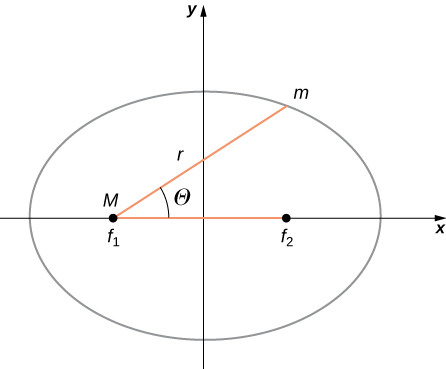
The variables r and $\theta$ are shown in [link] in the case of an ellipse. The constants $\alpha$ and e are determined by the total energy and angular momentum of the satellite at a given point. The constant e is called the eccentricity. The values of $\alpha$ and e determine which of the four conic sections represents the path of the satellite.

One of the real triumphs of Newton’s law of universal gravitation, with the force proportional to the inverse of the distance squared, is that when it is combined with his second law, the solution for the path of any satellite is a conic section. Every path taken by m is one of the four conic sections: a circle or an ellipse for bound or closed orbits, or a parabola or hyperbola for unbounded or open orbits. These conic sections are shown in [link] .