13.4 Satellite orbits and energy  (Page 42/8)

The Moon orbits Earth. In turn, Earth and the other planets orbit the Sun. The space directly above our atmosphere is filled with artificial satellites in orbit. We examine the simplest of these orbits, the circular orbit, to understand the relationship between the speed and period of planets and satellites in relation to their positions and the bodies that they orbit.

Circular orbits

As noted at the beginning of this chapter, Nicolaus Copernicus first suggested that Earth and all other planets orbit the Sun in circles. He further noted that orbital periods increased with distance from the Sun. Later analysis by Kepler showed that these orbits are actually ellipses, but the orbits of most planets in the solar system are nearly circular. Earth’s orbital distance from the Sun varies a mere 2%. The exception is the eccentric orbit of Mercury, whose orbital distance varies nearly 40%.

Determining the orbital speed    and orbital period    of a satellite is much easier for circular orbits, so we make that assumption in the derivation that follows. As we described in the previous section, an object with negative total energy is gravitationally bound and therefore is in orbit. Our computation for the special case of circular orbits will confirm this. We focus on objects orbiting Earth, but our results can be generalized for other cases.

Consider a satellite of mass m in a circular orbit about Earth at distance r from the center of Earth ( [link] ). It has centripetal acceleration directed toward the center of Earth. Earth’s gravity is the only force acting, so Newton’s second law gives

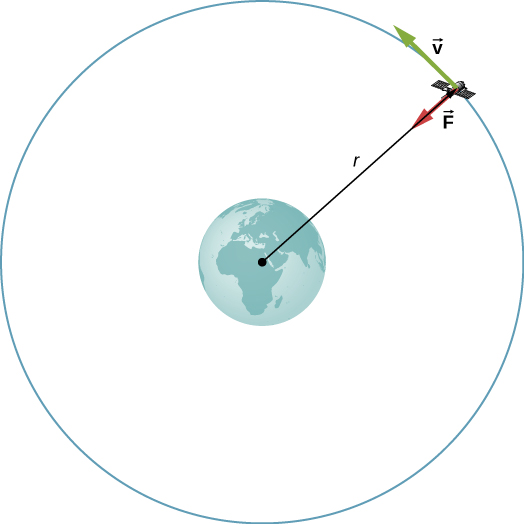
We solve for the speed of the orbit, noting that m cancels, to get the orbital speed

Consistent with what we saw in [link] and [link] , m does not appear in [link] . The value of g , the escape velocity, and orbital velocity depend only upon the distance from the center of the planet, and not upon the mass of the object being acted upon. Notice the similarity in the equations for $v_{\text{orbit}}$ and $v_{\text{esc}}$ . The escape velocity is exactly $\sqrt{2}$ times greater, about 40%, than the orbital velocity. This comparison was noted in [link] , and it is true for a satellite at any radius.

To find the period of a circular orbit, we note that the satellite travels the circumference of the orbit $2\pi r$ in one period T . Using the definition of speed, we have $v_{\text{orbit}}=2\pi r\text{/}T$ . We substitute this into [link] and rearrange to get

We see in the next section that this represents Kepler’s third law for the case of circular orbits. It also confirms Copernicus’s observation that the period of a planet increases with increasing distance from the Sun. We need only replace $M_{\text{E}}$ with $M_{\text{Sun}}$ in [link] .

We conclude this section by returning to our earlier discussion about astronauts in orbit appearing to be weightless, as if they were free-falling towards Earth. In fact, they are in free fall. Consider the trajectories shown in [link] . (This figure is based on a drawing by Newton in his Principia and also appeared earlier in Motion in Two and Three Dimensions .) All the trajectories shown that hit the surface of Earth have less than orbital velocity. The astronauts would accelerate toward Earth along the noncircular paths shown and feel weightless. (Astronauts actually train for life in orbit by riding in airplanes that free fall for 30 seconds at a time.) But with the correct orbital velocity, Earth’s surface curves away from them at exactly the same rate as they fall toward Earth. Of course, staying the same distance from the surface is the point of a circular orbit.