| << Chapter < Page | Chapter >> Page > |
(iv) For block of mass, “ ” :
We need to eliminate “ ” and solve two equations for “ ”. For this we multiply first by “ ” and second by “ ”. The new pair of equations are,
Adding, we have :
Substituting for “ ”, we have :
Problem 3 : Two blocks of mass “m” and “nm” are part of the arrangement involving pulley and incline as shown in the figure. If friction is negligible everywhere and mass of the pulleys and the strings are also negligible, then find the acceleration of the mass “nm”.
Incline and pulley system
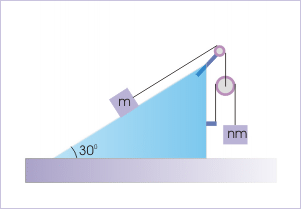
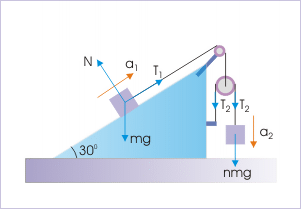
Solution : Here, we see that block of mass “m” is connected to the moving pulley by a single string. Hence, their accelerations are equal in magnitude. Let the acceleration of the block of mass “m” be “ ” and the acceleration of block of mass “nm” be “ ”. Similarly, let the tensions in the two strings be “ ” and “ ” respectively. The force diagrams of the elements of the system are shown here.
Incline and pulley system
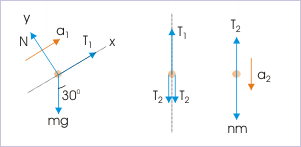
The free body diagrams of block on the incline, moving pulley and hanging block are shown here :
Free body diagrams
Now, we need to establish the relation between accelerations of pulley and block of mass “nm” by applying constraint analysis. For this we consider a horizontal reference passing through the fixed end of the string. Using length of string as constraint, we have :
Incline and pulley system
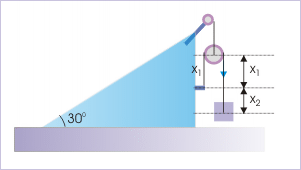
Differentiating w.r.t time twice, we have :
Comparing magnitude only,
We see that if one end of the string is fixed, then the acceleration of the other end of the string passing over a movable “mass-less” pulley is two times the acceleration of the movable pulley. Let,
Substituting for tension and acceleration in the equations of the blocks as derived earlier, we have
Multiplying second equation with 2 and adding to eliminate " ",
The acceleration of the block of mass “nm” is :
Problem 4 : In the arrangement shown, the masses are = 2 kg and = 4 kg. The mass of the strings and pulleys are negligible. The friction is negligible between block and fixed incline and also between pulley and string. Find the accelerations of two blocks.
Incline and pulley system
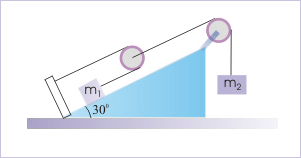
Solution : Considering free body diagram of the moving pulley, we see that tension in the string attached to mass “ ” is half of the tension attached to the moving pulley. Hence, if “T” be the tension in the string attached to block of mass “ ”, then the tension in the string attached to the pulley is “2T”.
Incline and pulley system
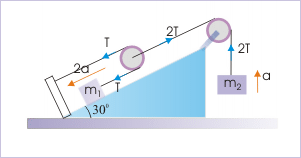
From, the constrain relation as derived in prevous example, we know that the acceleration of the block of mass “ ” is twice that of the pulley. Hence, if “a” be the acceleration of the moving pulley, then acceleration of the block of mass “ ” is “2a”.
The free body diagram of two blocks are shown here. The force analysis of the block of mass “ ” is :
Free body diagrams
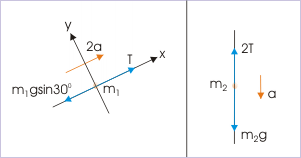
Similarly, force analysis of the block of mass “ ” is :
Adding two equations, we have :
Thus, accelerations of block are :
Author wishes to thank John Trautwein for making suggestions to improve this module.

Notification Switch
Would you like to follow the 'Physics for k-12' conversation and receive update notifications?