| << Chapter < Page | Chapter >> Page > |
Since energy in an isolated system is not destroyed or created or generated, one might wonder why we need to be concerned about our energy resources, since energy is a conserved quantity. The problem is that the final result of most energy transformations is waste heat transfer to the environment and conversion to energy forms no longer useful for doing work. To state it in another way, the potential for energy to produce useful work has been “degraded” in the energy transformation. (This will be discussed in more detail in Thermodynamics .)
What is the difference between energy conservation and the law of conservation of energy? Give some examples of each.
If the efficiency of a coal-fired electrical generating plant is 35%, then what do we mean when we say that energy is a conserved quantity?
Integrated Concepts
(a) Calculate the force the woman in [link] exerts to do a push-up at constant speed, taking all data to be known to three digits. (b) How much work does she do if her center of mass rises 0.240 m? (c) What is her useful power output if she does 25 push-ups in 1 min? (Should work done lowering her body be included? See the discussion of useful work in Work, Energy, and Power in Humans .
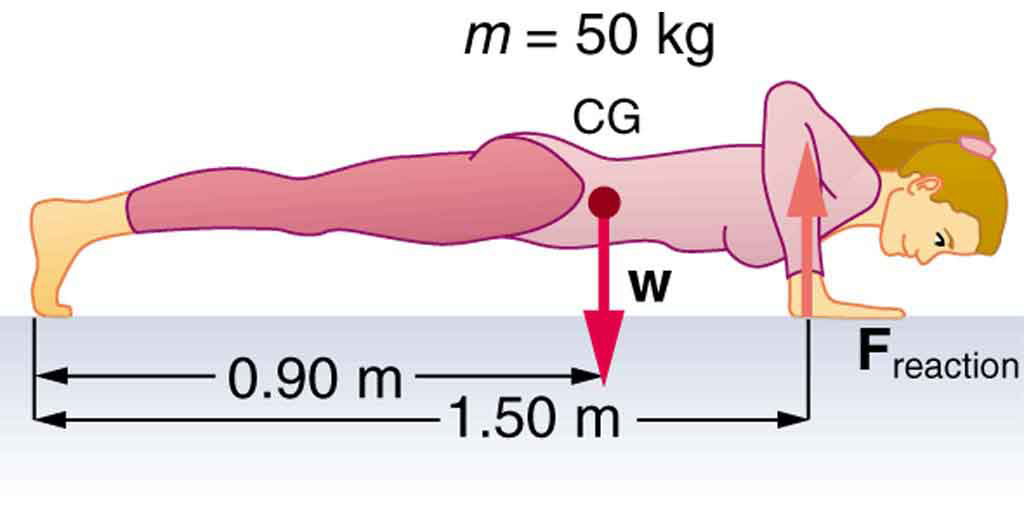
(a) 294 N
(b) 118 J
(c) 49.0 W
Integrated Concepts
A 75.0-kg cross-country skier is climbing a slope at a constant speed of 2.00 m/s and encounters air resistance of 25.0 N. Find his power output for work done against the gravitational force and air resistance. (b) What average force does he exert backward on the snow to accomplish this? (c) If he continues to exert this force and to experience the same air resistance when he reaches a level area, how long will it take him to reach a velocity of 10.0 m/s?
Integrated Concepts
The 70.0-kg swimmer in [link] starts a race with an initial velocity of 1.25 m/s and exerts an average force of 80.0 N backward with his arms during each 1.80 m long stroke. (a) What is his initial acceleration if water resistance is 45.0 N? (b) What is the subsequent average resistance force from the water during the 5.00 s it takes him to reach his top velocity of 2.50 m/s? (c) Discuss whether water resistance seems to increase linearly with velocity.
(a)
(b)
(c) Assuming the acceleration of the swimmer decreases linearly with time over the 5.00 s interval, the frictional force must therefore be increasing linearly with time, since . If the acceleration decreases linearly with time, the velocity will contain a term dependent on time squared ( ). Therefore, the water resistance will not depend linearly on the velocity.

Notification Switch
Would you like to follow the 'College physics for ap® courses' conversation and receive update notifications?