| << Chapter < Page | Chapter >> Page > |
Три бројни оски кои се нормални меѓу себе образуваат правоаголен тродимензионален координатен систем и определуваат тродимензионален простор кој накратко се нарекува простор.
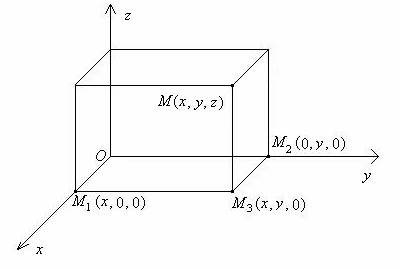 |
| Слика 1.1. Просторен координатен систем |
Секој пар координатни оски определува рамнина наречена координатна рамнина .
Во просторниот координатен систем се определуваат 3 координатни рамнини:
xOy координатна рамнина (определена со x -оската и y -оската);
xOz координатна рамнина (определена со x -оската и z -оската);
yOz координатна рамнина (определена со y -оската и z -оската).
Секоја точка M ( x , y , z ) која лежи на некоја од координатните рамнини или оски има координати:
| област | координати |
| xOy рамнина | ( x , y , 0) |
| xOz рамнина | ( x , 0, z ) |
| y О z рамнина | (0, y , z ) |
| x - оска | ( x ,0, 0) |
| y - оска | (0, y , 0) |
| z - оска | (0, 0, z ) |
Со координатните рамнини тродимензионалниот простор се дели на 8 делови наречени октанти . Знаците на координатите на произволна точка по октанти се:
| О ктант | З наци на координати |
| I | x > 0, y > 0, z > 0 |
| II | x < 0, y > 0, z > 0 |
| III | x < 0, y < 0, z > 0 |
| IV | x > 0, y < 0, z > 0 |
| V | x > 0, y > 0, z < 0 |
| VI | x < 0, y > 0, z < 0 |
| VII | x <0, y < 0, z < 0 |
| VIII | x > 0, y < 0, z < 0 |
Постојат величини кои се определуваат само со бројна вредност, додека други, освен со бројна вредност се определуваат уште и со правец и насока.
Дефиниција . Величините кои се определуваат само со бројна вредност се нарекуваат скалари .
Дефиниција . Величините кои се определуваат со бројна вредност, правец и насока се нарекуваат вектори .
Скаларни величини или накратко скалари се на пр. температурата, плоштината, должината и др. и тие се наполно определени со нивната бројна вредност. Затоа доволно е да се каже дека температурата на воздухот е 20 0 C, плоштината на некоја геометриска слика е 20 cm 2 , должината на отсечка е 5 m и тн.
Брзината е векторска величина и како таква е определена со бројна вредност, правец и насока. Затоа брзината со која дува ветерот се определува со бројната вредност на пр. нека таа е 5 m/s, во правец север-југ и во насока од север кон југ.
 |
| Слика 1.2. Вектори |
Според дефиницијата за вектор, секој вектор се дефинира со:
- интензитет (должина или модул) на вектор е растојанието помеѓу почетната и крајната точка на векторот и се означува со
;
- правец на векторот е правецот кој го определува правата на која лежи векторот и правата се нарекува носач на векторот;

Notification Switch
Would you like to follow the 'Векторска алгебра' conversation and receive update notifications?