| << Chapter < Page | Chapter >> Page > |
Find the slope of the line .
In order to find the slope of this line, we will choose any two points on this line.
Again, the selection of x and y intercepts seems to be a good choice. The x-intercept is (3, 0), and the y-intercept is (0, 2). Therefore, the slope is
The graph below shows the line and the intercepts: and .
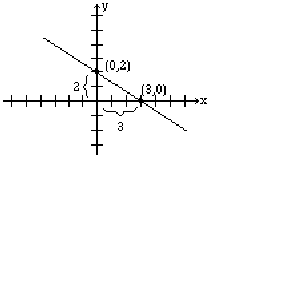
Find the slope of the line .
We again find two points on the line. Say (0, 2) and (1, 5).
Therefore, the slope is .
Look at the slopes and the y-intercepts of the following lines.
| The line | Slope | y-intercept |
| 3 | 2 | |
| -2 | 5 | |
| 3/2 | -4 |
It is no coincidence that when an equation of the line is solved for , the coefficient of the term represents the slope, and the constant term represents the y-intercept.
In other words, for the line , is the slope, and is the y-intercept.
Determine the slope and y-intercept of the line .
We solve for .
The
The .
In this section, you will learn to:
So far, we were given an equation of a line and were asked to give information about it. For example, we were asked to find points on it, find its slope and even find intercepts. Now we are going to reverse the process. That is, we will be given either two points, or a point and the slope of a line, and we will be asked to find its equation.
An equation of a line can be written in two forms, the slope-intercept form or the standard form .
The Slope-Intercept Form of a Line:
A line is completely determined by two points, or a point and slope. So it makes sense to ask to find the equation of a line if one of these two situations is given.
Find an equation of a line whose slope is 5, and y-intercept is 3.
In the last section we learned that the equation of a line whose slope = m and y-intercept = b is .
Since , and , the equation is .
Find the equation of the line that passes through the point (2, 7) and has slope 3.
Since , the partial equation is .
Now can be determined by substituting the point (2, 7) in the equation .
Therefore, the equation is .
Find an equation of the line that passes through the points (–1, 2), and (1, 8).
So the partial equation is
Now we can use either of the two points (–1, 2) or (1, 8), to determine .
Substituting (–1, 2) gives
So the equation is
Find an equation of the line that has x-intercept 3, and y-intercept 4.
x-intercept = 3, and y-intercept = 4 correspond to the points (3, 0), and (0, 4), respectively.
So the partial equation for the line is
Substituting (0, 4) gives
Therefore, the equation is .
The Standard form of a Line:
Another useful form of the equation of a line is the Standard form.

Notification Switch
Would you like to follow the 'Linear equations' conversation and receive update notifications?